拜占庭共识中的“蜜獾”

大名鼎鼎的异步共识论文《The Honey Badger of BFT Protocols》的笔记（异步真令人绝望.jpg）

加密货币在高度对抗的环境中茁壮成长，在这种环境中，预计会有动机明确的恶意攻击。出于这个原因，许多比特币的热心支持者将其称为“货币中的蜜獾”。

• 论文自称其为拜占庭共识中的“蜜獾”，足见其想法之大。

The Honey Badger of BFT Protocols

论文背景

• FLP 不可能定理：在纯异步环境下不可能存在一种确定性的共识协议

  • 做出一些更强的时序假设
  • 使用随机性的共识协议 ✅

• 做出一些更强的时序假设

  • 从网络分区中恢复得很慢：一个节点崩溃了，网络被暂时分割，持续时间为 $2^D\Delta$。修复网络后， 协议必须等待另一个 $2^(D+1)\Delta$ 的间隔才能开始选举一个新的领导者

  • 稳健性和响应性之间的权衡：参数 $\Delta$ 的选取是复杂的

论文贡献

• 时序假设被证明是脆弱的

  • 明确地构建了一个对抗性 “间歇同步 ”网络，使得 PBFT 等弱同步协议陷入停顿

• 实用异步拜占庭共识

  • 提出了 HoneyBadgerBFT，这是第一个在异步情况下提供最佳渐进效率 $𝑂(N)$ 的 BFT 原子广播协议。
  • 乐观情况下实验，PBFT 可达到的吞吐量随着节点数量的增加而减少，而 HoneyBadgerBFT 的吞吐量大致保持不变。
  • PBFT 在面对对抗性 “间歇同步 ”网络时将实现零吞吐量，而HoneyBadgerBFT 将以正常的速度完成周期。

构建对抗性 “间歇同步 ”网络

• 对抗性 “间歇同步 ”网络由调度器控制

• 调度器构建思路

  • PBFT 协议在很大程度上依赖于弱同步网络的有效性。如果没有取得进展，要么是因为领导者有问题，要么是因为网络停滞不前。而节点就会试图选举一个新的领导者
  • 对 PBFT 的攻击，调度器不会丢弃或重新排序任何消息，而只是延迟将消息传递到当前领导者的任何节点

• 调度器构建步骤

  • 首先，我们假设有一个节点崩溃了。然后，每当一个正确的节点成为领导者时，网络就会延迟消息，阻止进展，并导致下一个节点以轮流的方式成为新的领导者
  • 当崩溃的节点成为下一个领导者时，调度器立即修复网络分区，并在诚实的节点之间非常迅速地传递消息；然而，由于领导者已经崩溃，这里也没有取得进展

对抗性 “间歇同步 ”网络实例

• 符号定义

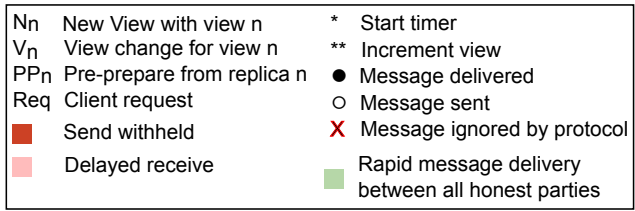
$0\Delta$ → $1\Delta$ → $3\Delta$ → $7\Delta$，原因是 PBFT 每次视图切换后，超时间隔翻倍

$0\Delta$ 阶段

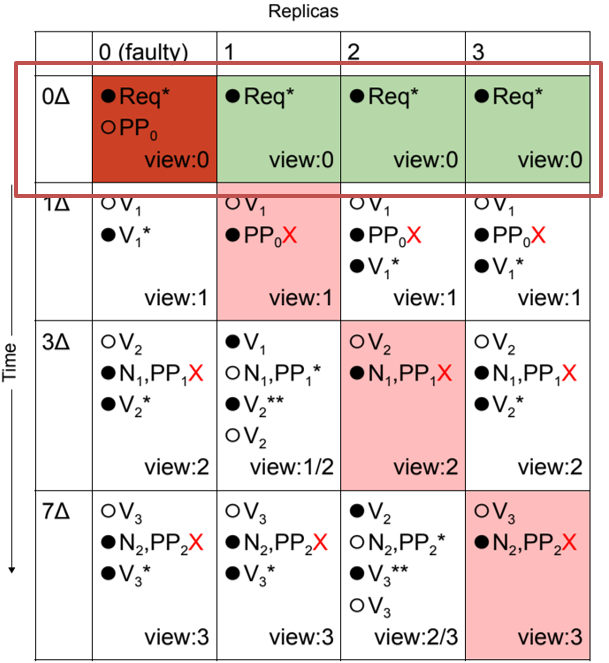
• 故障副本 0 最初是领导者，它会保留 PRE_PREPARE 消息的时间超过超时时间 $\Delta$

• 这会触发所有节点增加其视图计数器并为视图编号 1 广播 VIEW_CHANGE 消息

$1\Delta$ 阶段

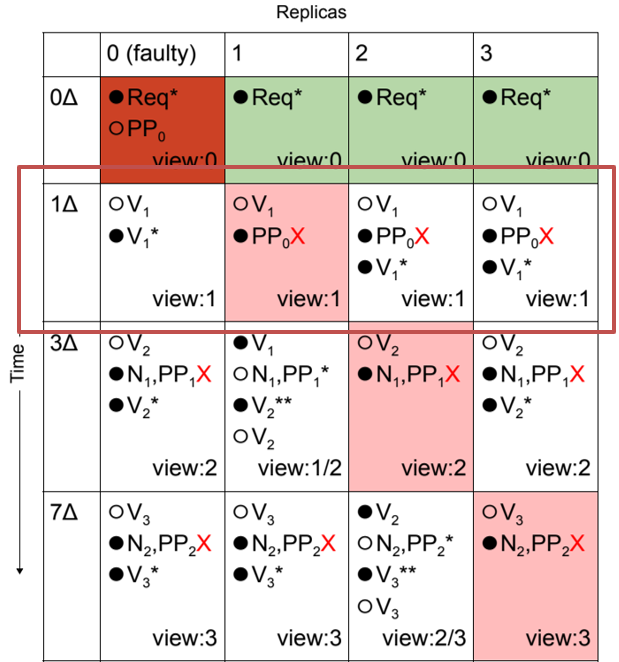
• 调度器推迟了所有 VIEW_CHANGE 消息对副本 1（视图 1 的领导者）的传递
• 其余节点的视图改变操作超时，因为它们没有从副本 1 收到有效的 NEW_VIEW 消息

$3\Delta$ 阶段

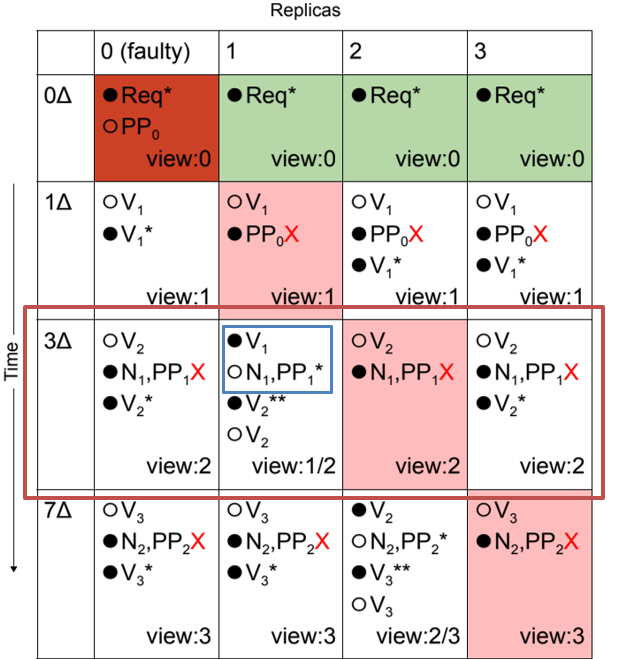
• 节点 0、2 和 3 将他们的视图计数器增加到 2，并广播另一个 VIEW_CHANGE 消息
• 此时，视图 1 的 VIEW_CHANGE 消息被传递给副本 1，副本1通过在视图 1 中广播一个 NEW_VIEW 和一个 PRE_PREPARE 消息来回应

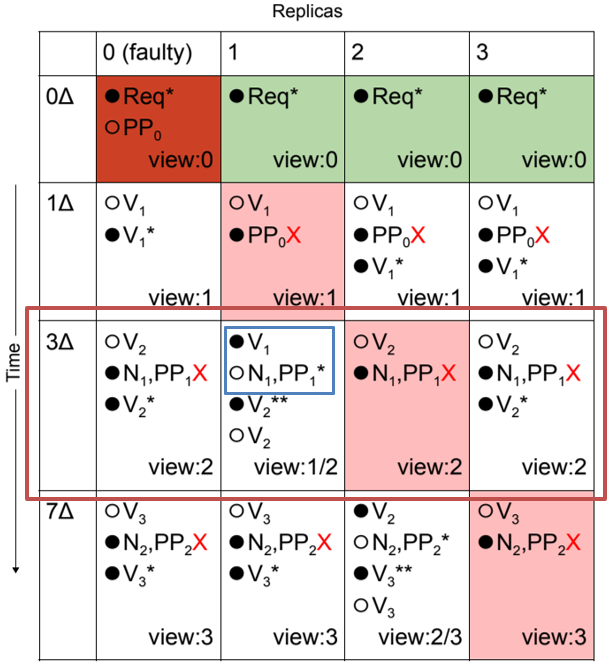
• 副本 1 通过在视图 1 中广播一个 NEW_VIEW 和一个 PRE_PREPARE 消息被所有其他节点忽略，因为它们已经进展到了视图编号 2
  然后，副本 1 将收到视图 2 的 VIEW_CHANGE 消息，并相应增加其视图计数器

$7\Delta$ 阶段

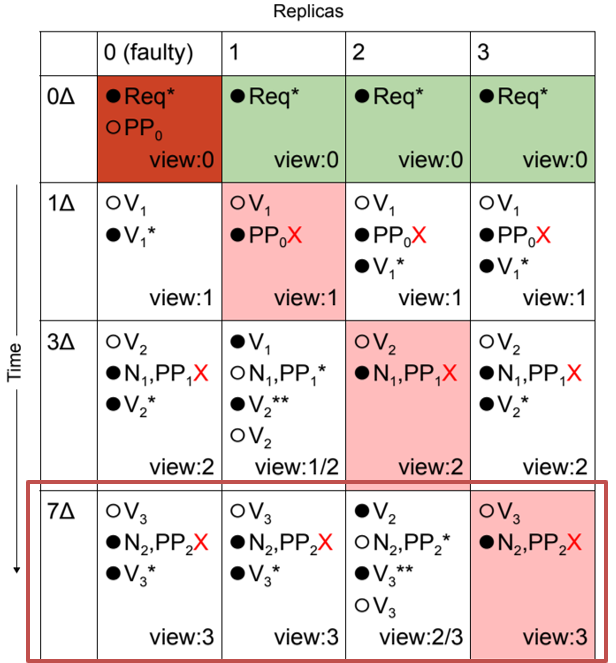
• 调度器会推迟所有 VIEW_CHANGE 消息对副本 2 的传递，确保所有其他节点的视图改变操作再次超时
• 这个过程将持续到有问题的副本 0 再次被选为领导者，这时调度器将加速传递所有消息，而副本 0 则扣留相应的 NEW_VIEW 和 PRE_PREPARE 消息以触发另一个视图变化，并重复这个循环

只要调度器扣留预定的非故障领导者的 VIEW_CHANGE 消息的时间超过（指数级增加的）超时间隔，这个循环就可以无限期地继续下去，阻止任何视图改变成功，并阻止协议取得任何进展。

HoneyBadgerBFT 方案

• 模型假设

  • 纯异步网络：
  • 静态拜占庭故障：$3ｆ+1\leq N$
  • 受信任的设置：初始设置阶段与受信任的密钥分发者交互

• 分布式计算中的共识等价问题

  • 相等问题
    • 原子广播：Hadzilacos and Toueg, 1994
    • 状态机复制：Schneider, 1990
  • 相关问题
    • 集群管理：Guerraoui and Schiper, 2001
    • 非阻塞原子提交：Guerraoui and Schiper, 2001

HoneyBadgerBFT 方案实际上是实现了原子广播

原子广播

• 原子广播协议必须满足以下属性，所有这些属性都应在异步网络中以高概率成立，并且不受任意对手的影响
  • 一致性：如果任何正确的节点输出交易 $\mathrm{tx}$，那么每个正确的节点都输出 $\mathrm{tx}$（安全性）
  • 全序性：如果一个正确的节点输出了交易序列 $\left\langle\mathrm{tx}_0, \mathrm{tx}_1, \ldots \mathrm{tx}_j\right\rangle$ ，而另一个正确的节点输出了 $\left\langle\mathrm{tx}_0^{\prime}, \mathrm{tx}_1^{\prime}, \ldots \mathrm{tx}_j^{\prime}\right\rangle$，则对 $i \leq \min \left(j, j^{\prime}\right)$， 有 $\mathrm{tx}_i=\mathrm{tx}_i^{\prime}$ 成立（安全性）
  • 抗审查攻击：如果一个交易 $\mathrm{tx}$ 被输入到 $N-f$ 个正确的节点，那么它最终会被每个正确的节点输出（活性）

总体设计

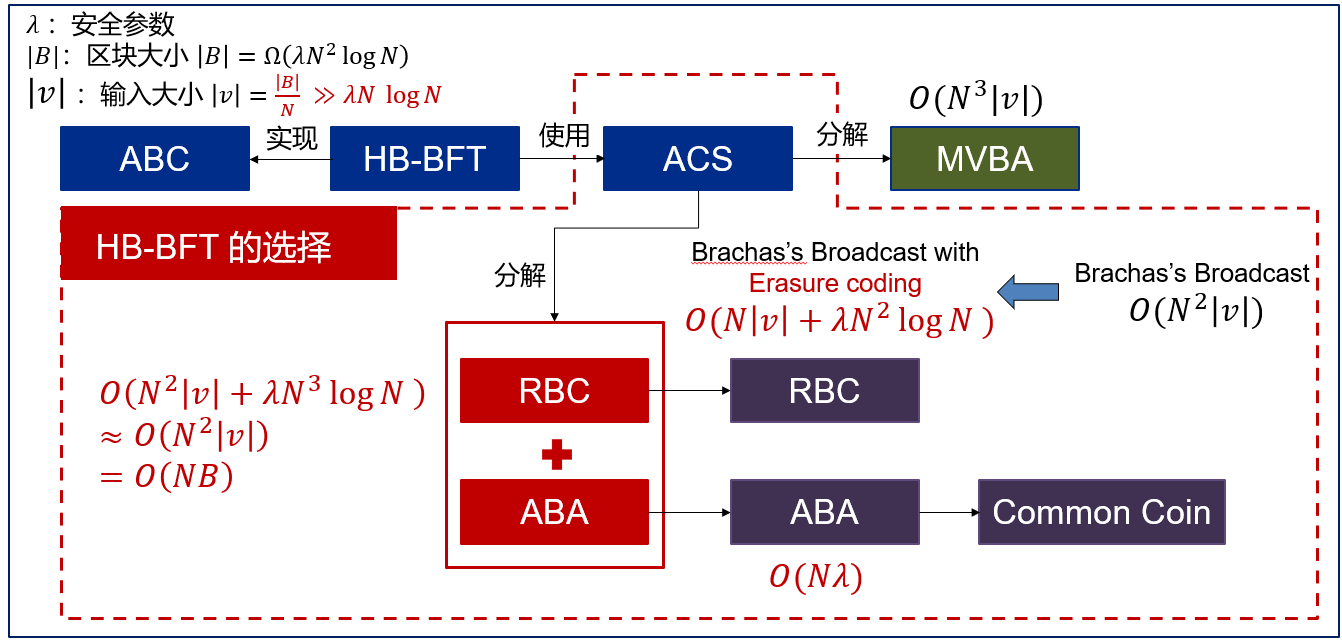
• HoneyBadgerBFT 通过 ACS(Asynchronous Common Subset, 异步公共子集) 实现了 ABC(Atomic Broadcast, 原子广播)。ACS 可以通过 MVBA(Multi-value Validated Byzantine Agreement, 多值拜占庭共识) 实现，但是 MVBA 原始协议有 $O(N^3|v|)$ 的开销，所以论文考虑了另一条路线。（DumboBFT 实际就是继续把 MVBA 这条路走下去了）

• 另一条路，RBC(Reliable Broadcast, 可靠广播) + ABA(Asynchronous Binary Agreement, 异步二元共识) 。通过纠错码，RBC 的复杂度从 $O\left(N^2|v|\right)$ 下降到了 $O\left(N|v|+\lambda N^2 \log N\right)$。ABA 基于 CC(Common Coin, 公共掷币) 实现，复杂度为 $O(N \lambda)$

• 因此，当输入大小 $|v|=\frac{|B|}{N} \gg \lambda N \log N$ 时，总时间复杂度约为 $O\left(N^2|v|\right)$

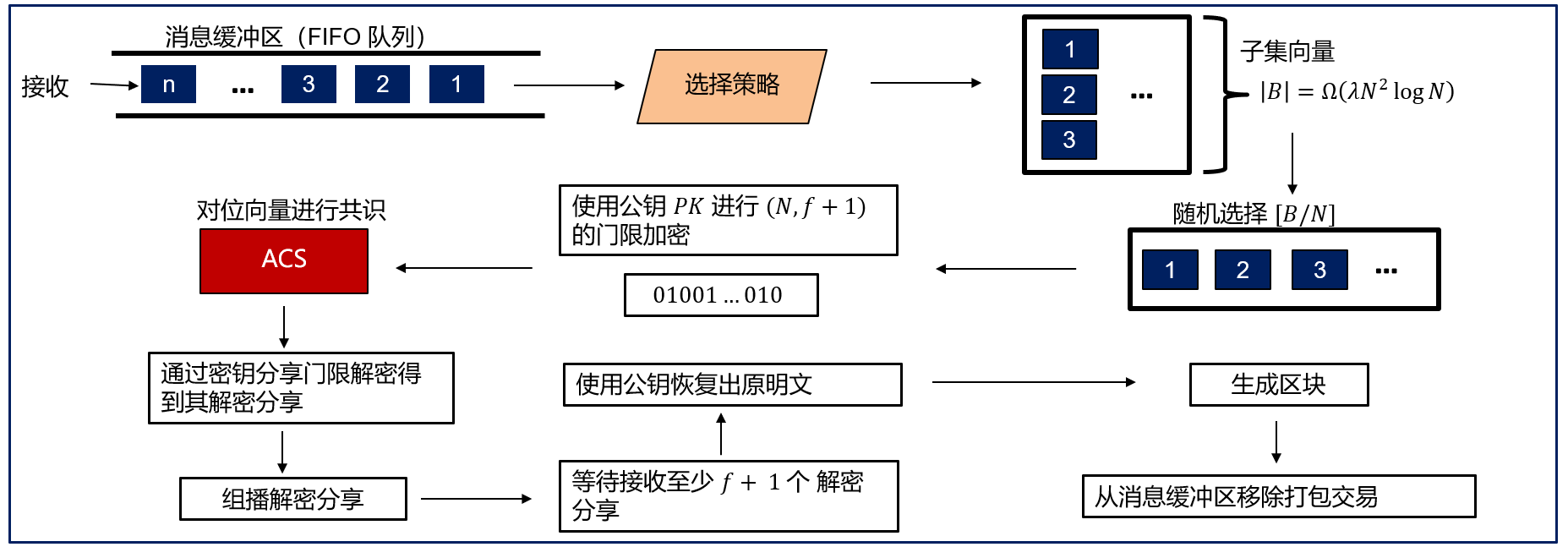
1. 每个节点首先从本地的交易池中选取前 $|B|$ 个合法的交易，之后再从这 $|B|$ 个交易中随机选择 $|B/N|$ 笔交易作为自己的提案

• 每个节点只选择 [𝐵/𝑁] 笔交易是为了降低通信复杂度
• 采用随机选取的方式，是为了降低每个节点选择重复交易的概率

2. 通过一个共享公钥通过门限加密将提案加密，交易的内容直到共识结束后（收到了来自 𝑓+1 个 解密分享）才能被解密

• 采用门限加密的方式，是为了防止审查攻击

3. 每个节点将加密后的提案作为 ACS 模块的输入，输出就得到了一个“名单”，记录了有哪些节点提交的提案成功得到共识。

4. 之后通过一系列的解密操作就得到了最终确认的区块。

异步公共子集 ACS

• 一个 ACS 协议满足以下属性：
  • 有效性: 如果一个正确的节点输出一个集合 $v$ ，那么 $|v| \geq N-f$ 且 $v$ 包含至少 $N-2 f$ 个正确节点的输入。
  • 一致性：如果一个正确的节点输出 $v$ ，那么每个节点都输出 $v$ 。
  • 全局性：如果 $N-f$ 个正确节点接收到一个输入，那么所有正确节点都会产生一个输出。

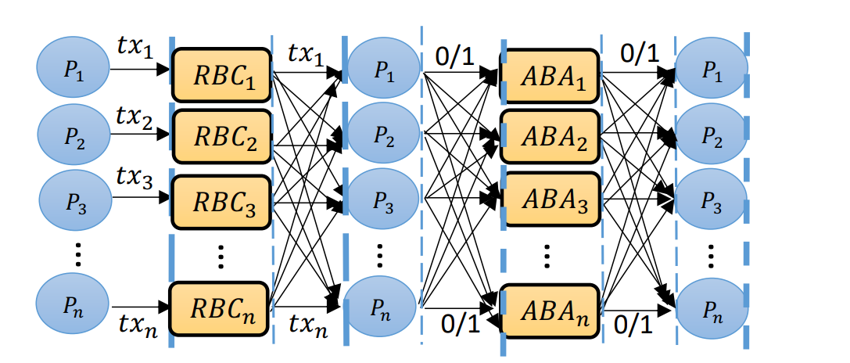
• 使用 Ben-Or 提出的 ACS 实现：通过 RBC 广播交易，通过 ABA 形成一致的二进制交易表
  • 每个节点都通过一个 RBC 协议广播自己的输入值（总共 $n$ 个并发的 RBC 协议）
  • 与此同时所有节点并发运行 $n$ 个 ABA 协议来决定在共识结果中输出哪些节点广播的输入值。

• 算法 ACS（对于某一参与方 $\mathcal{P}_i$）
  • 让 $\left\{RBC_i\right\}_N$ 指代可靠广播协议的 $N$ 个实例，其中 $\mathcal{P}_i$ 是 $RBC_i$ 的发送方。让 $\left\{BA_i\right\}_N$ 指代二元共识协议的 $N$ 个实例。

1. 在接收到输入 $v_i$ 后，将 $v_i$ 输入 $RBC_i$

2. 在从 $RBC_j$ 传送 $v_j$ 时，如果尚未向 $BA_j$ 提供输入，则向 $BA_j$ 提供输入 1。

3. 在从至少 $N-f$ 个 BA 实例传递值 1 时，向尚未提供输入的每个 $BA$ 实例提供输入 0。

4. 一旦 $BA$ 的所有实例都完成，令 $C \subset [1 . . N]$ 为每个交付 1 的BA 的索引。等待每个 $RBC_j$ 的输出 $v_j$ 使得 $j \in C$。最后输出 $\cup_{j \in C} v_j$。

等待每个 $RBC_j$ 的输出 $v_j$ 使得 $j \in C$。是因为正确的节点可能会观察到广播以不同的顺序完成

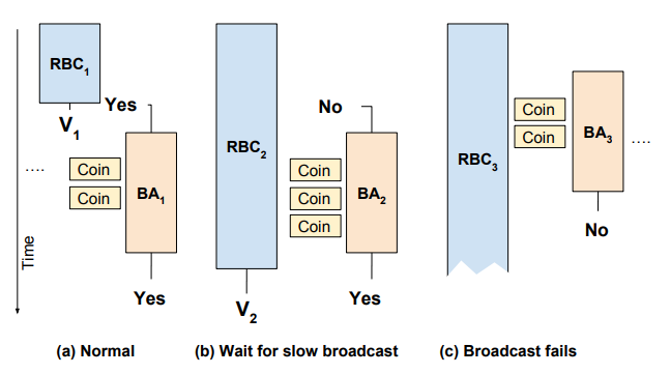
• a. $\mathrm{RBC}_1$ 结束比较早: 相对应的 $\mathrm{ABA}_1$ 的输入为 1， 其输出也 是 1
• b. $\mathrm{RBC}_2$ 结束的比较慢: 节点已经收到 $N-f$ 个输出 1，所以 对于 $\mathrm{ABA}_2$ 的输入为 0 。但由于其它个节点已经观察到 $\mathrm{RBC}_2$ 成功完成，对于 $\mathrm{ABA}_2$ 的输入为 1。因此节点最终对 对于 $\mathrm{ABA}_2$ 输 入 1，且等待 $\mathrm{RBC}_2$ 完成
• c. $\mathrm{RBC}_3$ 失败：直到 $\mathrm{RBC}_3$ 完成之前， $\mathrm{BA}_3$ 输出 0

可靠广播 RBC

• ACS 使用 RBC 确保源节点能够可靠地将消息发送到所有节点，一个 RBC 协议满足以下属性：
  • 一致性：任意两个正确节点都收到来自源节点的相同的消息
  • 全局性：只要有一个节点收到了来自源节点的消息，那么所有正确的节点最终都能收到这个消息
  • 可信性：如果源节点是正确的，那么所有正确的节点收到的消息一定与源节点发送的消息一致

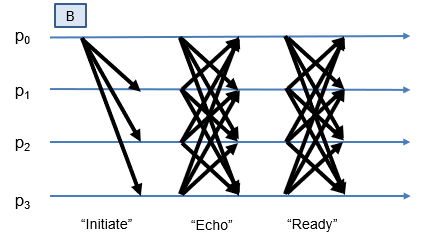
• 使用 Cachin 等人提出的基于纠删码的 RBC 实现:

  • 采用了 $(N-2 f, N)$ 纠删码 + Merkle 树模式
  • 消息传递的模式仍然跟传统的 RBC 类 似，主要分成 Initiate、Echo、Ready 三个阶段，其中后两个阶段各经历一次 all-to-all 的广播
  • 复杂度 $O\left(N|v|+\lambda N^2 \log N\right)$ 指导区块大小选择

• 纠删码：利用所有节点的带宽来平衡了 Leader 的带宽消耗

• 算法 RBC（对于某一参与方 $\mathcal{P}_i$，发送方 $\mathcal{P}_{sender}$）
• Initiate 阶段
  • 发送者 $\mathcal{P}_{sender}$ 将加密后的交易块 $v$ 作为 RBC 的输入， 使用 $(N-2 f, N)-$-纠删码技术生成 $N$ 个数据块 $\left\{s_i\right\}$
  • 利用 $\left\{S_j\right\}$ 计算出默克尔树根 $h$ 和 $\left\{S_j\right\}$ 到 $h$ 的路径 $\left\{b_j\right\}$
  • 发送 $\mathbf{VAL}\left(h, b_j, s_j\right)$ 到 $\mathcal{P}_j$
• Echo 阶段
  • 收到 $\mathbf{VAL}\left(h, b_j, s_j\right)$, 广播 $\mathbf{ECHO}\left(h_2 b_j, s_j\right)$ 到各方 $\left\{\mathcal{P}_j\right\}$
• Ready 阶段
  • 收到 $\mathbf{ECHO}\left(h, b_j, s_j\right)$ ，用默克尔树校验消息是否有效
  • 当节点收到来自 $N-f$ 个节点的有效 ECHO $\left(h, \cdot,\cdot\right)$, 选取 $N-2 f$ 个 ECHO 重新计算 $h^{\prime}$ 判断是否等于 $h$ ，如果相等且未发送过，则广播 $\mathbf{READY}(h)$ 消息
  • 当节点收到 $f+1$ 个 READY $(h)$ ，如果末发送过 $\mathbf{READY}(h)$ 消息，则广播 $\mathbf{READY}(h)$ 消息
  • 当节点收到 $2 f+1$ 个 $\mathbf{READY}(h)$ ，等待 $N-f$ 个有效 $\mathbf{ECHO}\left(h, \cdot,\cdot\right)$ ，得到交易块 $v$

异步二元共识 ABA

• ACS 使用 ABA 让所有节点对于 0 或 1 达成共识，一个 ABA 协议满足以下属性：

  • 一致性：所有正确节点的输出相同
  • 最终性: 如果所有正确节点都收到了输入，那么所有正确节点最终都会得到输出
  • 可信性：如果任意正确节点的输出是 $b$(0 或 1)，那么至少有一个正确节点的输入是 $b$

• 使用 Moustefaoui 等人提出的基于公共掷币 CC 的 ABA 实现：

  • 当节点无法达成一致的时候借助一个外部的随机源 CC 做决定
  • 使用 Cachin 等人基于门限签名方案的公共硬币 CC 实现
  • 以 $1 − 2^{−k}$ 的概率在 $O(k)$ 轮内完成协议

• 算法 CC
  • sid 被假定为一个唯一的随机数，用作这个公共硬币的 “明文”
  • (可信设置阶段)：可信第三方生成公共公钥以及密钥分享，密钥分享发送给各方。
  • 被调用 GetCoin 时，广播 $ThresholdSign n_{k}(s k_i, sid)$
  • 当收到至少 $f+1$ 个密钥共享时，将其生成签名 Sig，签名检验成功则输出签名

一点想法

• HoneyBadgerBFT 称自己的方案为 “cherry-pick”，这点确实不假。几乎可以如剥洋葱一样，找到每一层算法的来源。