密码学备忘
本文最后更新于 2026年1月28日 晚上
自己在学习密码学课程时做的总结,AES 那一部分写得比较简略
密码学备忘
引言
-
密码学的意义
-
密码学基础
- 对称密码
- 公钥密码
- 数据完整性算法
- 相互信任
安全概述
-
CIA三元组
-
保密性(数据保密性、隐私性)
-
完整性(数据完整性、系统完整性)
-
可用性
※:真实性、可追溯性
-
-
安全攻击
- 安全威胁:
- 自然威胁
- 人为威胁
- 主动攻击: 拒绝服务、消息修改、伪装、重放
- 被动攻击(窃听):信息内容的泄露,流量分析
- 安全威胁:
-
安全服务:(OSI安全体系结构)安全服务通过安全机制来实现安全策略
- 数据保密性:防止被动攻击
- 认证:保证通信的真实性
- 数据完整性:功能与保护对象有关
※:满足完整性业务,不一定同时满足认证性,因为敌手可以假冒合法用户发送满足完整性的数据包 - 不可否认性
- 访问控制
-
基本安全设计准则
-
攻击面和攻击树
- 攻击面:网络由系统中一系列可访问且可利用的漏洞组成,包括网络攻击面、软件攻击面、人类攻击面
- 攻击树:采用分支化、层次化表示来利用安全漏洞的可能技术集合的数据结构
- 根节点:攻击的目的
- 叶节点:发起攻击的不同方式
- 与节点: 该节点的所有子节点代表的字母表都必须优先完成
- 或节点: 需要至少完成应该子目标
网络安全模型
- 信息流安全基本模型:
- 消息的安全变换(基本成分): 包括对消息的加密和认证
- 通信双方共享的秘密信息(基本成分)
- 一个可行的第三方(可选成分):分发密钥建立安全通道、仲裁
- 安全网络通信需要考虑的4个要素:
- 加密、认证算法
- 用于算法的秘密信息:密钥、秘密参数等
- 秘密信息的分发与共享
- 使用加密、认证算法和密钥以获得安全服务所需的协议(安全协议)
- 防止未授权访问的模型:守卫者和内部控制部件构成两道防线
- 信息安全的三个层次:系统安全、数据安全(密码技术)、内容安全(不良内容过滤)
传统加密技术
- 密钥 (密钥空间即 的可能值范围)——加解密密钥不一定相同
- 明文:
- 密文:
- 加密函数:
- 解密函数:
对称密码模型
(传统密码/常规密码/私钥密码/单钥密码/conventional/private-key/single-key)
- 发送方和接收方共享同一个密钥
- 基本成分:明文(plaintext)、加密算法(encryption)、密钥(key)、密文(cipher)、解密算法(decryption)
- 保证安全的两个条件:加密算法足够强、保证密钥安全
- Kerckhoff原则:系统的保密性不依赖于对加密体制或算法的保密,而依赖于对密钥的保密(这也降低了保密成本)
密码编码学(cryptography)
- 特征:
- 转换明文为密文的运算类型(不允许信息丢失,即运算均可逆):代替(映射)/置换 (重新排列)
- 所用的密钥数:单密钥密码(基于计算安全性,运行速度快,但是不便于密钥管理)/双密钥密码(基于可证明安全性,便于密钥的管理,还可用于消息认证,但是运行速度慢)
- 处理明文的方法
- 分组(块)密码:按组处理,l每次处理一组元素。适合数据库加密,组内有错误扩散;一般用于公开的理论研究。
- 序列(流)密码:连续处理输入元素,每次输出一个元素。加解密速度快,无错误扩散;一般用于实际的安全产品
密码分析学(cryptanalytics)
- 典型目标:得到密钥,而不是仅仅得到单个密文对应的明文
攻击传统密码体制的一般方法
-
穷举攻击:对一条密文尝试所有可能的密钥,知道把它转化为可读的有意义的明文。平均而言,成功至少需要尝试所有可能密钥的一半。
-
密码分析:利用算法的性质和明文的特征或某些明密文对
| 攻击类型 | 攻击者已知的东西 |
| 唯密文攻击 | 加密算法 待破译的密文 |
| 已知明文 | 加密算法 待破译的密文 由密钥形成的一个或多个明文-密文对 |
| 选择明文 | 加密算法 待破译的密文 由破译者选择的明文信息,连同对应的由密钥生成的密文 |
| 选择密文 | 加密算法 待破译的密文 由破译者选择的猜测性密文,连同对应的由密钥生成的已破译明文 |
| CCA-1攻击(午餐攻击):有限的解密机(得到目标密文之后不能再使用) | |
| CCA-2攻击(凌晨攻击):无限的解密机(得到目标密文之后能继续使用) | |
| 选择文本 | 加密算法 待破译的密文 由破译者选择的明文信息,连同对应的由密钥生成的密文 由破译者选择的猜测性密文,连同对应的由密钥生成的已破译明文 |
-
加密算法要经得住已知明文攻击
-
分析依据
对称密码:明文的结构和模式在加密之后仍然保存了下来,能在密文中找到一些蛛丝马迹
公钥密码:密钥对的数学性质
- 无条件安全:如果算法产生的密文不能给出惟一决定相应明文的足够信息。此时无论敌手截获多少密文、花费多少时间,都不能解密密文
- Shannon指出,仅当密钥至少和明文一样长时,才能达到无条件安全。(一次一密)
- 计算上安全:破译密文的代价超过被加密信息的价值或破译密文所花的时间超过信息的有用期
代替技术
- 代替法:将明文字母替换成其他字母、数字、符号的方法
恺撒密码 Caesar Cipher
加密算法:
解密算法:
- 加解密算法已知,密钥只有25个,适合穷举攻击
采样密码 Decimation Cipher
密文字母是将明文字母按下标每隔k位去除要给字母排列而成(字母表首尾相接),又称为乘法代替密码
加密算法:
- 在乘法代替密码中,当且仅当 , 才是一一映射
- 是,称为平凡密钥,此时所有字母映射到自身,不是一个合适的密钥
- 合适的密钥有 个
解密算法:
仿射代替密码
将移位代替密码和乘法代替密码结合起来就构成仿射代替密码
加密算法:,其中
- 当 ,就是乘法代替密码;当 ,就是移位代替密码
- 时,密钥空间大小为 个
解密算法:
单表代替密码
每个明文字母映射到一个不同的随机密文字母
- 可以选取一个英文短语,称为key word/key phrase,按顺序去掉重复字母,将它依次写在明文字母表下,将明文字母表中未在短语中出现过的字母依次写在短语之后,即构造出一个代替表。
- 密钥空间:,大于56位DES的密钥空间
- 看似安全,实则不然:可以基于语言统计规律进行破译
- 缺陷:密文带有原始字母使用频率的一些统计学特征,每个元素仅仅密文中的一个元素产生影响(解决:多个字母一起加密、多表代替)
语言的冗余与密码的分析(密码破译就是研究明文信息在密文信息中有多大程度泄露)
-
英文字母的出现频率大小排列顺序:E TAO INSHR DL CMWFGYPBU VK JXQX
-
双字母的出现频率大小排列顺序:th he in er an
-
三字母、数字、标点符号等等
-
冠词the
-
英文中一半的词以e,s,d,t结尾,以t,a,s,w开头
-
分析步骤:统计密报的一节统计特性,识别报文为单表密,然后利用猜字法
最著名的多字母代替密码——Playfair密码
把明文的双字母音节作为一个单元并将其转换为密文的“双字母音节”
- Playfair 密钥矩阵
- 5*5字母矩阵
- 从左往右,从上到下:填充key word,用其他字母填写剩下的空缺
- I=J
| M | O | N | A | R |
|---|---|---|---|---|
| C | H | Y | B | D |
| E | F | G | I/J | K |
| L | P | Q | S | T |
| U | V | W | X | Z |
-
加密规则
- 明文字母(填充):2个字母分为一组,不够则添加一个字母
- 同行字母对加密:循环向右,ei→FK
- 同列字母对加密:循环向下:cu→EM
- 其他字母加密:矩形对角线字母,且按行排序,hs→BP
-
解密规则:加密的逆向操作
-
安全性:优于简单的单表代替密码,难用频率分析字母;但是密文中仍含有明文的部分结构信息,给定几百个字母即可被攻破
另一个多字母代换密码——Hill Cipher
加密方法是由 个线性方程(矩阵)决定的,方程中每个字母被指定为一个数值
加密算法:1. 明文分组并编码 2. ,其中 为密钥矩阵, 分别为明、密文分组
解密算法:1. 密文分组并编码 2.
- 完全隐藏了单字母的频率特性(连续m个明文替换成m个密文)
- 所用矩阵越大所隐藏的频率信息越多
- 足以抵抗唯密文攻击,但是不能抵抗已知明文攻击
多表代替密码 Polyalphabetic Ciphers
令明文字母表为 , 为代替表序列,明文 ,则相应的密文为:
- 若 是非周期的无限序列,则相应的密码为非周期多表代替密码
- 对于每个明文字母都采用不同的代替表进行加密,称之为一次一密密码(one-time pad cipher)
- 实际中多采用周期多表代替密码
维吉尼亚密码 Vigenère Cipher
设明文为 ,密钥为 ,密文
加密算法:
-
-
查表法
博福特密码 Beaufort Cipher
加密算法:
解密算法:(完全相同!)
对应的Vigenère cipher:
弗纳姆密码 Vernam Cipher
-
选择择随机二元数字序列作为密钥,以 表示
-
文字母变成二元向量后也可以表示成二元序列 , 和 分别记录在穿孔纸带上。
-
加密算法:将 和 的相应位逐位模2相加,即
-
解密算法:
-
这种加密方式如果使用电子器件实现,就是一种序列密码
-
如果采用的密钥不重复就是一次一密体制,理论上不可破,但是实际上不可行
周期多表代替密码的破译
- 判断加密类型是单表代替密码还是多表代替密码
- 粗糙度 :定义为每个密文字母出现的频率与均匀分布时每个字母出现的概率的离差的平方和。
- 对于英文字母而言,明文或单表代替密码的粗糙度为0.027, 一般密文的粗糙度将在0~0.027之间变化。
- 初步判定多表代替密码所用的密表数
- 重合指数I.C值:知道了I.C值就可以提取密钥字长或密表数的近似值信息
- 确定多表代替密码所用的密表数
- 移位法:对密文进行移位并和原来的密文进行逐位比较以求重码数,根据重码数来确定密表数
- 重复字模式分析法(Kasiski检验):计算密文中重复字模式的距离
- 密表匹配
※:转轮机
eg:German Enigma,Allied Hagelin,Japanese Purple
- 实现了复杂多变的多表代替密码,多层加密
- 每个圆柱体有26个输入、输出引脚,代表26个字母
- 单个圆柱体定义一个单表代换
- 每个圆柱体每次定义的单表代换算法不同
- 单个圆柱体定义了周期为26的多表代换
置换技术
栅栏技术:按对角线顺序写出明文,以行的顺序读出作为密文
- 改进:带有密钥,重复加密,多步置换
矩阵排列法:优先行/列置换
隐写术
- 不可见的墨水
- 打字机的色带校正
缺点:开销大,需要额外的付出来隐藏相对较少的信息;一旦被发现就完全没有价值 - 一个可选的方案:先加密,然后用隐写术隐藏
分组密码和数据加密协议
Feistel分组密码结构
- 理想分组密码:设每 个一组,不同的映射/代换(即密钥)有 种,每一种密钥的大小是 位(并不实用)
- Feistel 提出了一种近似体制:使用乘积密码的概念来逼近理想分组密码
乘积密码 Product Cipher
- 在单个加密机制中依次使用两个或两个以上不同类型的基本密码(如:代换和置换),所得结果的密码强度将强于每个单个密码的强度。
- 本质:开发一个分组密码,密钥长为 位,分组长为 位,采用 个变换
Claude Shannon and Substitution-Permutation Ciphers
-
1949年,Claude Shannon 引进了 substitution-permutation (S-P) networks 的思想,即现代的乘积加密器,形成了现代分组加密的基础
-
S-P Networks 基于代替和置换这两个基本操作,提供了对明文信息处理所做的混淆和扩散
-
Shannon认为,为了对付基于统计分析的密码破译,必须对明文作混淆和扩散处理,以减少密文的统计特性,为统计分析制造障碍
-
混淆 Confusion:尽可能使密文和加密密钥之间的关系变得复杂,以阻止攻击者发现密钥
-
扩散 Diffusion:让每个明文数字尽可能地影响多个密文数字,使明文的统计特性消散在密文中
-
-
Feistel建议交替使用代换和置换,增强密码的扩散和混淆性能
Feistel密码
-
加密算法:
令 为轮函数;令 分别为第 轮的子密钥。那么基本构造过程如下:
(1)将明文信息均分为两块:;
(2)在每一轮中,进行如下运算( 为当前轮数):
;
所得的结果即为:
-
解密算法:
对于密文 ,我们将 由 向 进行,即 。然后对密文进行加密的逆向操作,如下:
(1);
(2)
所得结果为 ,即原来的明文信息
-
依赖的参数和设计特点
- 分组大小:分组越大意味着安全性越高(如果其他条件相同),但加密/解密速度也越慢
- 密钥大小:密钥长度越长则安全性越高,但加密/解密速度也越慢
- 循环次数:一个循环不能保证足够的安全性,而循环越多 则安全性越高
- 子密钥产生算法 :算法越复杂则密码分析就应该越困难
- Round函数:复杂性越高则抗击密码分析的能力就越强
数据加密标准 DES
DES 的基本概念
-
Data Encryption Standard:1977年美国国家标准局公布的IBM公司研制的一种数据加密算法:数据加密标准
-
破译方法
- DES 受到的最大攻击是它的密钥长度仅有56比特
- 1990年 S.Biham 和 A.Shamir 提出了差分攻击的方法,采用选择明文 攻击,最终找到可能的密钥
- M.Matsui 提出的线性分析方法,利用 个已知明文,成功地破译了16圈 DES算法,到目前为止,这是最有效的破译方法
-
实现步骤:
- 给定明文 ,通过一个固定的初始置换 来排列 中的位,得到 。 。其中 由 前32位组成, 由 的后32位组成。
- 计算函数 的16次迭代, 根据下述规则来计算 。其中 是长为48位的子密钥。子密钥 是作为密钥 (56位)的函数而计算出的。
- 对比特串 使用逆置换 得到密文 。
-
DES 加密流程图
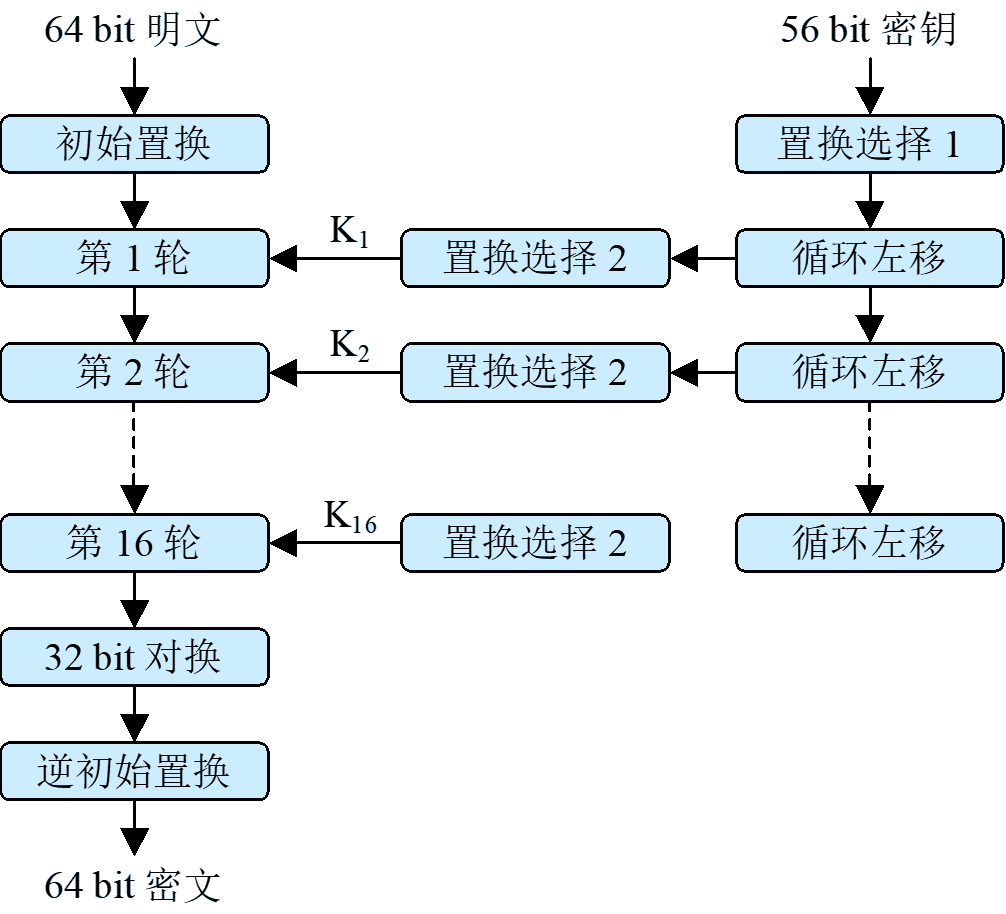
-
DES 一轮迭代
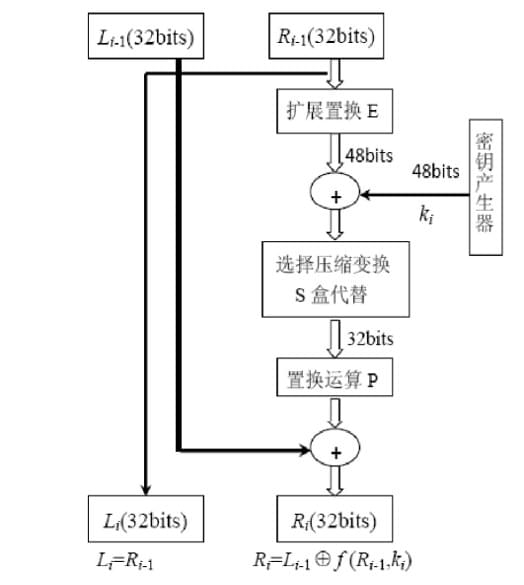
-
S盒选取
每一个S盒都接受6个比特作为输入并产生4个比特作为输出。
输入的第一和最后一个比特构成一个2位二进制数,用来选择由 表中的四行所定义的四种替代的一种,中间的4个比特则选出一列
-
子密钥的产生
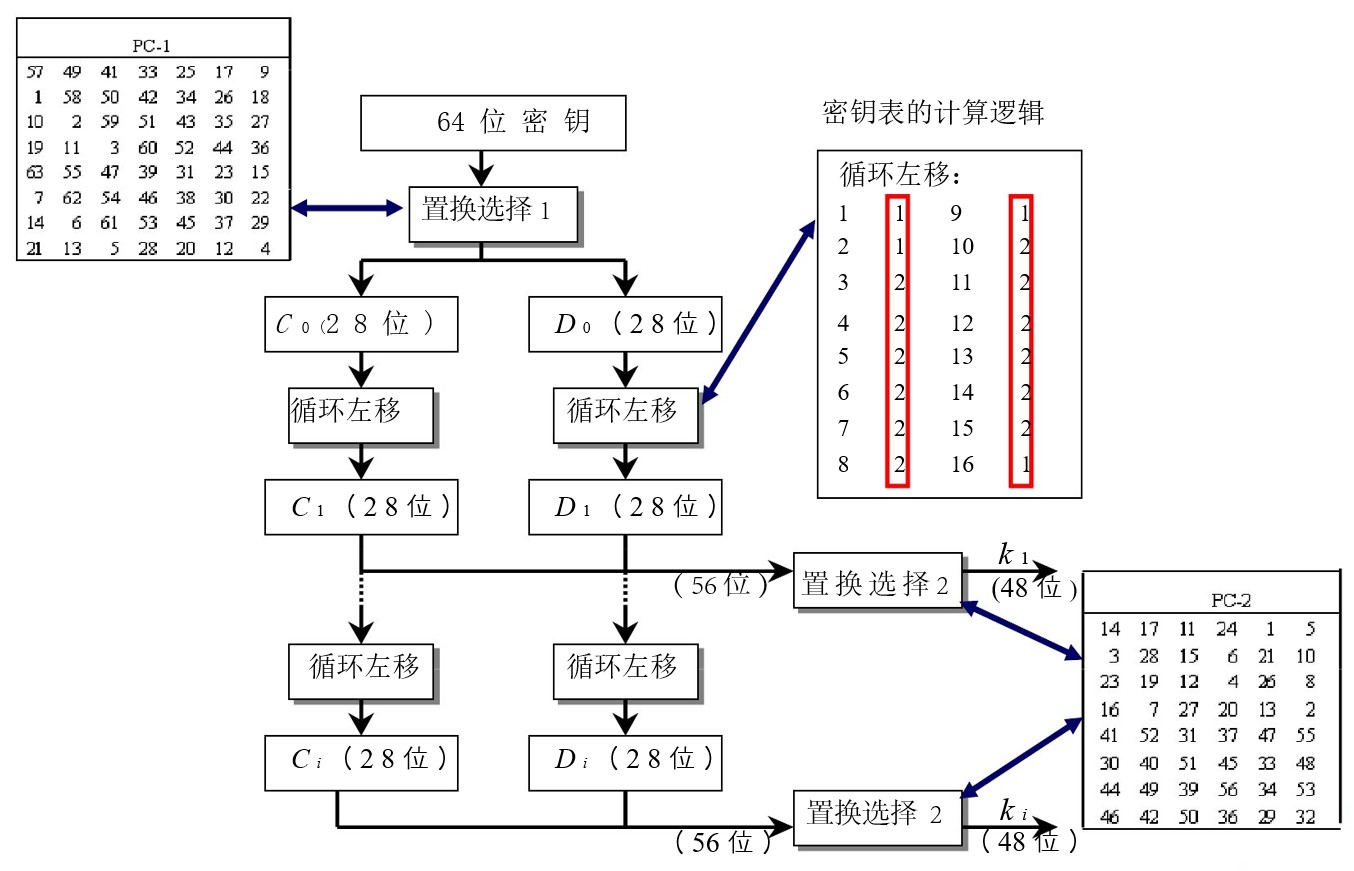
- 弱密钥:给定的初始密钥k产生的16个子密钥相同
- 半弱密钥:若存在种子密钥 ,使 ,则称 是半弱密钥,且称 与 是对合的
-
DES 的雪崩效应:(P置换的目的是提供雪崩效应) 明文或密钥的一点小的变动都引起密文的较大变化
-
攻击方法:差分密码分析攻击 线性密码分析
差分分析方法
- 对于 DES 的分析,可忽略初始置换 和 。
- 对DES 限制到 轮( )。
- 以 为明文,且以 作为 轮 DES 的密文。
- 对两个明文 和 ,规定它们的异或值为 ,整个讨论都使用撇号 ()表示两个比特串的异或值。 )表示两个比特串的异或值。
-
定义 1:设 是一个特定的 S盒 (),考虑长度为 的比特串的一个有序对 ,我们说 的输入 异或是 ,输出异或是
- 输入异或是长度为 的比特串 ,输出异或是长度为 的比特串 。
-
定义 2:对任何一 个 B_j^' \in (𝑍_2)^6=\left\{(a_0,a_1,a_2,a_3,a_4,a_5)|a_j\in \left\{0,1 \right \} \right \},定义集合 \Delta(B_j^') 是由输入异或为 B_j^' 的有序对 组成
-
对比特串 B_j^' 来说,集合 \Delta(B_j^') 包含 个有序对元素。有
这是因为 ,所以
-
对 \Delta(B_j^') 中的每一对,我们能够计算出 的输出异或,同时用表列出结果的分布。有 个输入异或,它们经 的输出分布在 种可能值中,这些分布的非均匀性,就是攻击 DES 的基础
-
表示一个 S 盒的所有可能对的输入异或盒输出异或分布的表称为该 S 盒的差分分布表
-
-
定义 3:对于长度 6 的比特串 和长度为 4 的比特串 ,定义
- 那些输出异或相同的 的集合
- 考虑一般的情况:对于 的 8 个 S 盒的每一个盒有 64 可能的输入异或,于是有 512 个分布
-
定义 4:设 和 是长度为 6 的比特串, 是长度为 4 的比特串,定义 , 是 的形式。
- 假设 是 S 盒 的两个输入, 的输出异或为 ,记为 ,那么密钥比特 出现在集合 之中。
-
3 轮 DES 的差分攻击模式:
输入:,其中
- 计算:
- 计算: 和
- For j in range(0,8) 计算:
三重 DES
- 设 是一个密码算法,如果对任意的密钥 ,,都存在密钥 ,使得对任意的明文 有:,则称 是闭合的。显然,
※:1992年,K.W. Campbell,M.J. Wiener 证明了 DES 不是一个群。
正因以上结论,二重 DES,三重 DES 有一定的价值,其穷举攻击的安全性虽有所改进,然而并非2倍,3倍的密钥量那么坚强
-
中途相遇攻击法
若有明文密文对 满足
则可得
给定一已知明密文对 ,可按下述方法攻击:
-
以密钥 的所有 个可能的取值对此明文 加密,并将密文 存储在一个表中;
-
从所有可能的 个密钥 中依任意次序选出一个对给定的密文 解密,并将每次解密结果 ,在上述表中查找相匹配的值。一旦找到,则可确定出两个密钥 和 ;
-
以此对密钥 和 对另一已知明文密文对 中的明文 进行加密,如果能得出相应的密文 就可确定 和 是所要找的密钥。
eg:
-
对于给定明文,以两重DES加密将有 个可能的密文。
-
可能的密钥数为 个。所以,在给定明文下,将有 个密钥能产生给定的密文。
-
用另一对64bits明文密文对进行检验,就使虚报率降为 。
-
这一攻击法所需的存储量为 Byte,最大试验的加密次数 。这说明破译双重DES的难度为 量级。
-
三重DES加密
加密算法:
解密算法:
称其为加密-解密-加密方案,简记为EDE(encrypt-decrypt-encrypt)。
高级加密标准 AES
评估要求:安全性、计算效率、内存要求、使用简便性、灵活性
-
AES 是一个迭代型分组密码,分组长度固定为 128 比特,密钥长度则可以是 128,192 或 256 比特
-
Rijndael 是一个迭代型分组密码,分组长度和密钥长度均可以是 128,192 或 256 比特
-
AES加密过程涉及到4种操作,分别是字节替代、行移位、列混淆和轮密钥加。
解密过程分别为对应的逆操作。
加解密中每轮的密钥分别由初始密钥扩展得到。算法中16个字节的明文、密文和轮密钥都以一个4x4的矩阵表示。
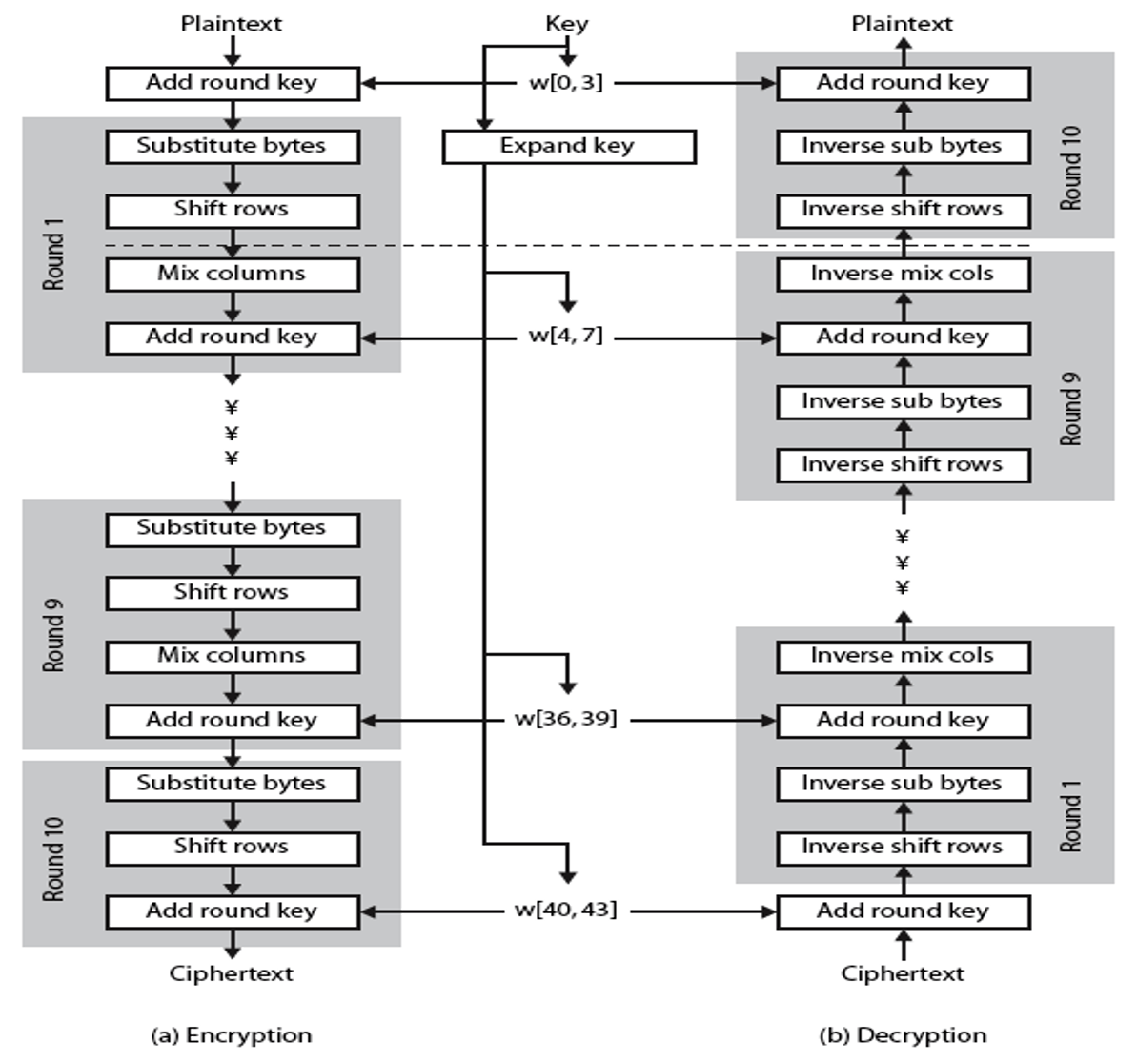
字节替代 SubBytes
-
它独立地将状态中的每个字节利用代换表(S盒)进行运算
-
S盒被设计成能够抵挡所有已知的攻击
-
S盒是由16×16个字节组成的矩阵,包含了8位值所能表达的256种可能的变换
-
※ DES:S: 6→4 AES: 8→8
-
-
State中的每个字节按照如下的方式映射为一个新的字节:将该字节的高4位作为行值,低4位作为列值,然后取出S盒中对应行列交叉处的元素作为输出
S盒的构造方法
-
逐行按照上升排列的方式初始化 S 盒。第一行是 ;第二行是 等,在 x 行 y 列的字节值是 ;
-
把S盒中的每个字节映射为它在有限域 上的乘法逆;其中,元素 映射到它自身 ;
-
把S盒中的每个字节表示为 8位,对 S 盒中的每个字节中的每个位做如下变换:
其中,对于 ,是字节的第 位, 是值为 或 的字节 c 的第 i 位
行移位
- 行移位变换完成基于行的循环移位操作,变换方法为:第0行不变,第1行循环左移1个字节,第2行循环左移两个字节,第3行循环左移3个字节
列混淆
- 利用GF(28)域上算术特性的一个代替,同样用于提供算法的扩散性
- 列混淆:左乘列混淆矩阵
- 计算方式:
- ,为 本身
- , 的二进制左移一位(右边补0),如果溢出(即如果 的二进制最高位为1),那么再异或上
- ,结果为
- : 的二进制位 ,左移一位得到 ,因为本身的二进制最高位为 ,所以再异或 ,即 ,得到 即:
- 计算方式:
轮密相加
- 在轮密钥加中,128 位的 state 按位与 128 位的轮密钥 XOR
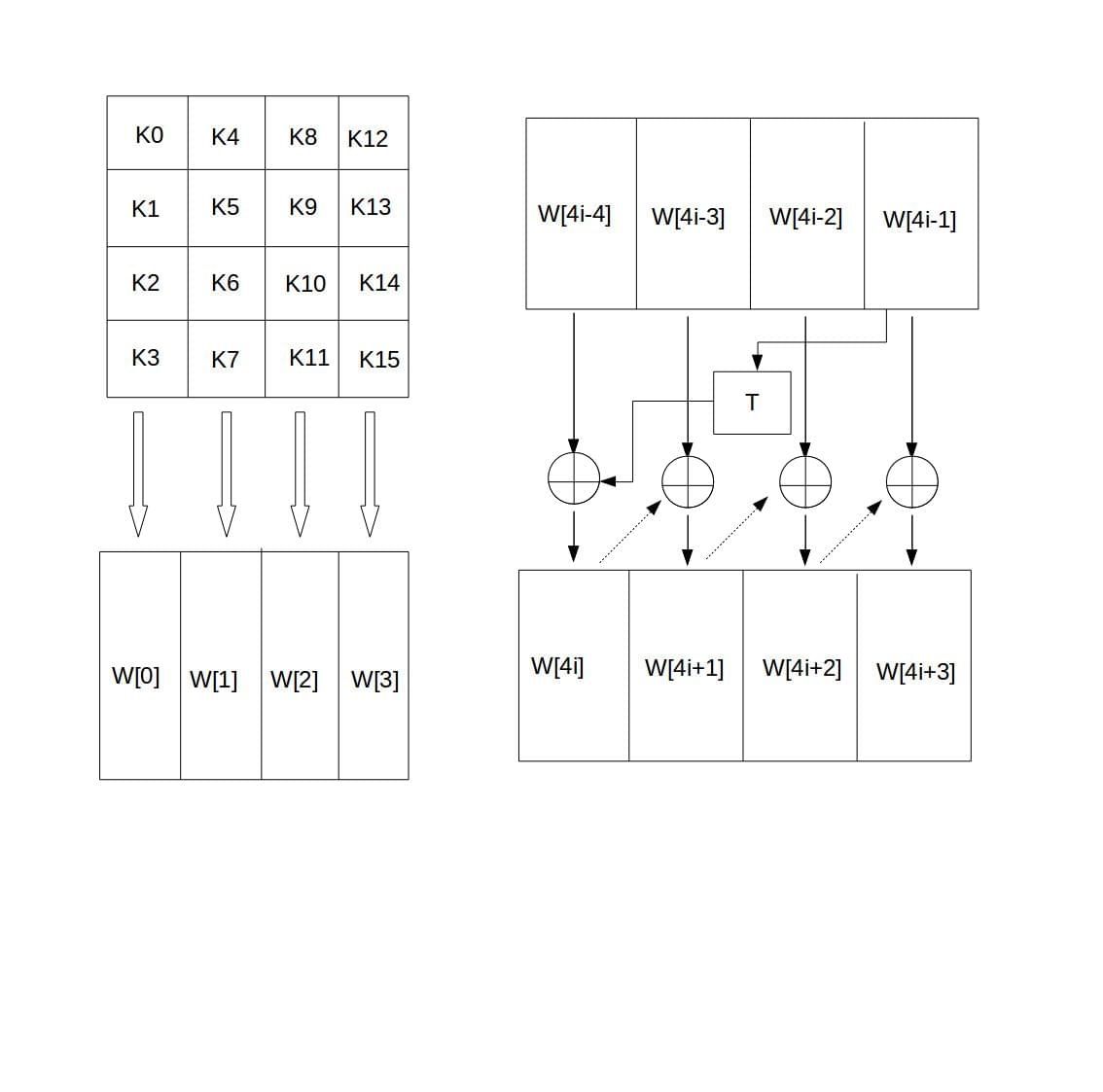
密钥扩展
分组加密的工作模式
问题引入:每次使用相同的密钥对多个分组加密,会引发许多安全问题
工作模式简介
-
工作模式:是一项增强密码算法或者使算法适应具体应用的技术,如将分组密码应用于数据块组成的序列或者数据流
-
初始化向量 IV:许多工作模式中用于随机化加密的一块数据,因此可以有相同的密文、相同的密钥产生不同的密文而无需重新产生密钥。一般无需保密。
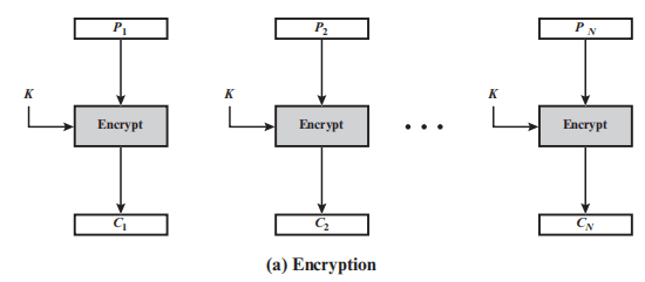
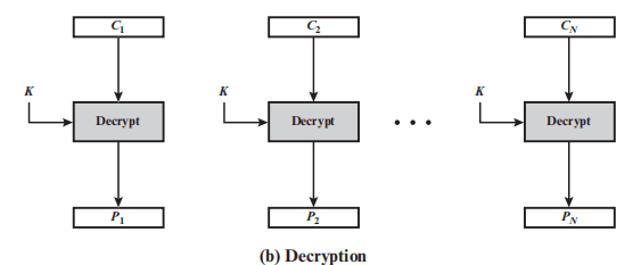
电码本 ECB 模式
-
ECB 模式是最简单的运行模式。
-
直接利用加密算法分别对分组数据组加密
-
一次处理一组明文分块,每次使用相同的密钥加密
-
-
特点:在给定的密钥下,同一明文组总产生同样的密文组
-
往往需填充
-
ECB 用于短数据(如加密密钥)时非常理想,因此如需安全传递DES、AES 等密钥,ECB是最合适的模式
- ECB 用于长消息时可能不够安全:如果消息有固定结构,密码分析者有可能找出这种关系。
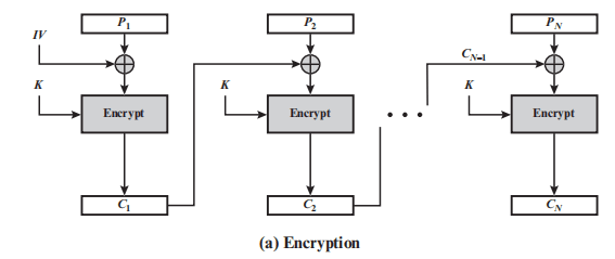
密文分组连接模式 CBC
-
加密算法的输入是当前明文分组和前一次密文分组的异或
-
串行,不能并行化
-
明文有一组有错,以后的密文组都受影响
加密:
-
解密时,每一个密文分组被解密后,再与前一个密文分组异或
-
两个邻接的密文块即可得到一个明文块,可以并行化(错误不传播)
解密:
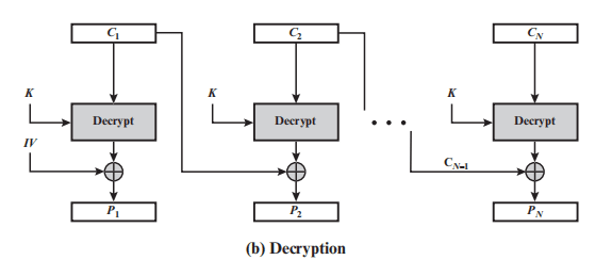
- 同样需要填充
- IV 对于收发双方都应是已知的,为使安全性最高,IV 应像密钥一样被保护,可使用 ECB 加密模式来发送IV
- 保护 IV 的原因:敌手篡改 IV 中的某些比特,则接收方收到的相应的比特也发生了变化
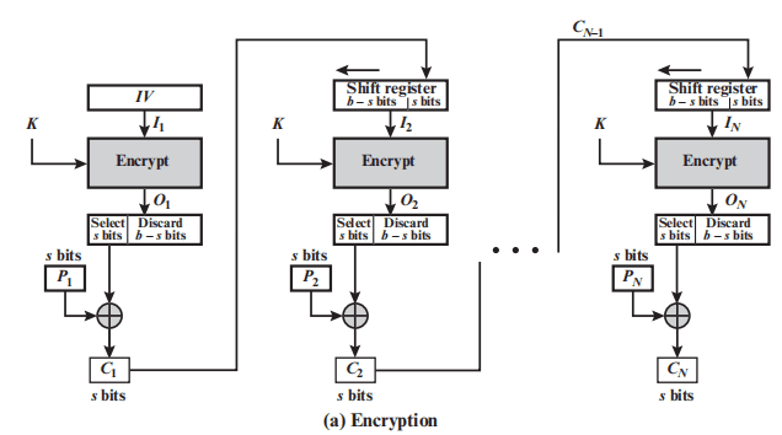
密文反馈模式 CFB
-
若待加密消息必须按字符(如电传电报)或按比特处理时,可采用CFB模式
-
利用 CFB 模式或 OFB 模式可将分组对称密码转换为流密码。流密码不需要对消息填充,而且运行是实时的
-
流密码具有密文和明文一样长这一性质,因此,如果需要发送的每个字符长为 8 比特,就应使用 8 比特密钥来加密每个字符。如果密钥长超过 8比特,则造成浪费。
-
加密过程:
-
加密函数的输入是 b 位的移位寄存器,其初值为某个初始向量 IV。
-
输出最左边的 s 位与明文的第一个分段 P1 异或得到密文的第一个单元 C1,发送 C1 ;
-
移位寄存器左移 s 位,C1 填入移位寄存器的最右边 s 位;
-
直至所有明文单元被加密完
- 串行,不能并行化
- 解密过程:
-
将收到的密文单元与加密函数的输出异或得到明文单元。
-
使用加密函数而非解密函数。
-
CFB 与 CBC 的区别是反馈的密文长度为 k ,且不是直接与明文相加,而是反馈至密钥产生器。
- 两个邻接的密文块即可得到一个明文块,可以并行化(错误不传播)
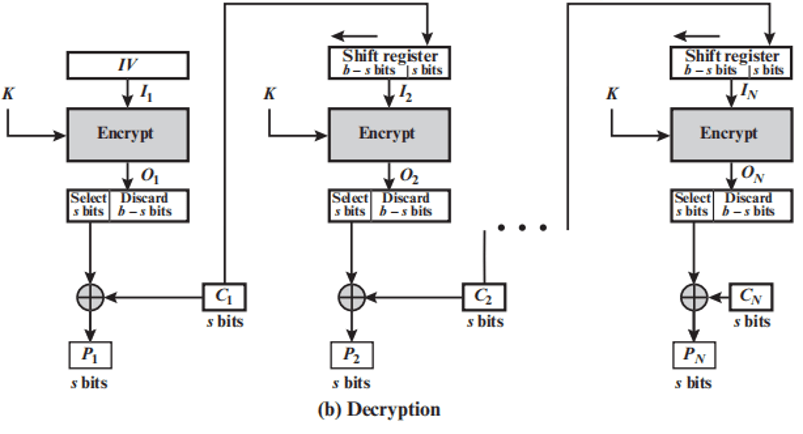
-
优点:
-
适合数据以比特或字节为单位出现,适合加密数据流;
-
能隐蔽明文数据图样,也能检测出对手对于密文的篡改;
-
仅需要实现加密算法;
-
CFB模式除能获得保密性外,还能用于认证。
-
-
缺点:
-
对信道错误较敏感,错误传播:1个比特密文传输错误会传播约64/j 个分组
-
CFB也需要一个初始矢量,并要和密钥同时进行更换**。**
-
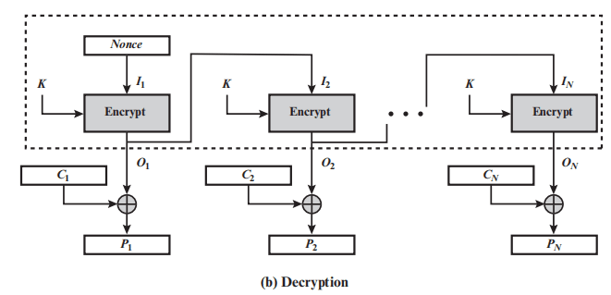
输出反馈模式 OFB
- OFB 模式的结构类似于 CFB
- 不同之处:OFB 模式是将加密算法的输出反馈到移位寄存器,而 CFB 模式中是将密文单元反馈到移位寄存器
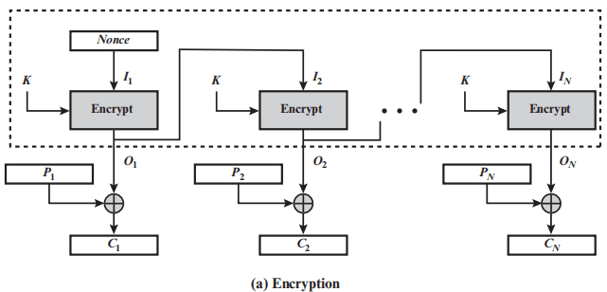
-
OFB的特点:
-
消息作为比特流,移位寄存器
-
分组加密的输出与被加密的消息相异或
-
只需要实现加密算法
-
不适合认证
-
-
预处理加密输出分组之后可以并行
-
优点:传输过程中的比特错误不会被传播,
-
适合有扰信道,比如卫星等
-
缺点:
-
比 CFB 模式更易受到对消息流的篡改攻击
如在密文中取1比特的补,那么在恢复的明文中相应位置的比特也 为原比特的补。因此使得敌手有可能通过对消息校验部分的篡改和对数据部分的篡改,而以纠错码不能检测的方式篡改密文。 -
不具有自同步能力,要求系统要保持严格的同步
-
计数器模式 CTR
- CTR 模式:与 OFB 相似,CTR 将块密码变成流密码。它通过递增要给加密计数器已产生连续的密钥流
- 可并行
工作模式对比
| 模式 | 描述 | 用途 |
|---|---|---|
| 电码本(ECB)模式 | 每个明文组独立地以同一密钥加密 | 传送短数据(如一个加密密钥) |
| 密码分组链接(CBC) | 加密算法的输入是当前明文组与前一密文组的异或 | 传送数据分组;认证 |
| 密码反馈(CFB)模式 | 每次只处理输入的 j 比特,将上一次的密文作加密算法的输入以产生伪随机输出,该输出再与当前明文异或以产生当前密文 | 传送数据流;认证 |
| 输出反馈(OFB)模式 | 与 CFB 类似不同之处是本次加密算法的输入为前一次加密算法的输出 | 噪声信道(如卫星通信)传送数据流 |
| 计数器(CTR)模式 | 对计数器依次用 k 加密后与明文异或 | 适合并行,可随机访问 |
伪随机数的产生和流密码
随机数的使用
大量基于密码学的网络安全算法和协议都使用了二进制随机数,如:
-
密钥分发和相互认证方案。如在密钥分配中,需使用时变值进行握手以防止重放攻击。时变值使用随机数可以防止攻击者判断或者猜测出时变值
-
会话密钥的产生。用随机数作为会话密钥
-
公钥密码算法中密钥的产生。用随机数作为公钥密码算法中的密钥,或以随机数来产生公钥密码算法中的密钥
-
用于对称流密码加密的位流的产生
随机数源
-
真随机数:很难获得
- 物理噪声产生器,如:离子辐射脉冲检测器、气体放电管、漏电容等
- 将高质量的随机数作为随机数库编辑成书
-
伪随机数:使用算法来生成随机数。
随机数的产生要求
-
随机性
以下两个准则常用来保障数列的随机性:
-
分布均匀性:序列中的位分布应是均匀的,即0和1出现的频率大约相等;
-
独立性:序列中任何子序列不能由其他子序列推导出。
- 序列是否满足均匀分布可通过检测得出,而是否满足独立性则无法检测,相反却有很多检测方法能证明序列不满足独立性
-
-
不可预测性
- 在设计密码算法时,由于真随机数难以获得,经常使用似乎是随机的序列(这样的序列称为伪随机数序列,这样的随机数称为伪随机数
对 PRNG 要求
-
通用要求:输出保密性——不知道种子的敌手不能决定伪随机串
-
特定要求:随机性、不可预测性、种子的特性
-
随机性:生成的位流尽管是确定的,但要显示随机。
- 没有单个的测试可以判定一个PRNG生成的数据具有随机性;
- NIST规定测试应建立三个特征:
- 均匀性:在产生随机或伪随机位序列的任何点,0或1出现的量大约相等,即每个出现的概率恰好为1/2
- 可伸缩性:用于序列测试的任何测试也可以用于从序列中抽取的子序列的测试
- 一致性:对于所有初始值(种子),发生器的行为必须具有一致性
-
不可预测性
-
前向不可预测性:如果不知道种子,那么不管知道序列中前面的多少位,都无法预测序列中的下一位;
-
后向不可预测性:从产生的任何值都不能推断出种子值
-
-
种子的要求:安全、不可预测
-
伪随机数发生器
线性同余发生器
-
线性同余法
-
参数
-
模数
-
乘数
-
增量
-
种子
-
-
随机数序列 按下面的迭代式获得:
-
-
线性同余发生器:定义 ,其中 ,称 为一个 线性同余生成器
-
评价线性同余算法的性能有以下3个标准:
- 迭代函数应是全周期的,即函数在重复之前应产生0到m-1之间的所有数
- 产生的序列看上去应是随机的
- 迭代函数能有效地利用32位运算器方便的实现
-
为使随机数数列的周期尽可能大,m应尽可能大,普遍原则是选 m 接近等于计算机能表示的最大整数
-
假定敌手能确定 ,就可通过以下方程组,
解出 a,c 和 m。
※:改进的方法:利用内部系统时钟修正随机数数列
-
每当产生N个数后,就利用当前的时钟值模m后作为种子
-
直接将当前的时钟值加到每个随机数上(模m加)
-
-
常用变形
- 幂形式:
- 离散指数形式:
-
BBS 发生器
-
已经证明过的密码强度最强的伪随机数产生器,
-
整个过程如下:
-
选:选择两个大素数 ,满足 p\equivq\equiv3 \bmod 4。
-
算:计算 。
-
选:选一随机数 ,使得 与 互素。
-
算:按以下算法产生比特序列 :
$$\mathrm{X}{0}=\mathrm{s}^{2} \bmod \mathrm{n}\
for\quad i=1 \quad to \quad\infty \quad do{\
\quad\begin{array}{l}
X{i}=X^{2}{i-1} \bmod n \
\left.B{i}=X_{i} \bmod 2\right}
\end{array}$$
即在每次循环中取Xi的最低有效位
- 如果伪随机比特产生器能通过下一比特检验,则称为密码安全伪随机比特产生器
- 即以伪随机比特产生器的输出序列的前 个比特作为输入,如果不存在多项式时间算法,能以大于1/2的概率预测第 个比特。
使用分组密码的伪随机数产生
-
推荐:CTR模式和OFB模式
-
使用分组密码工作模式的 PRNG
-
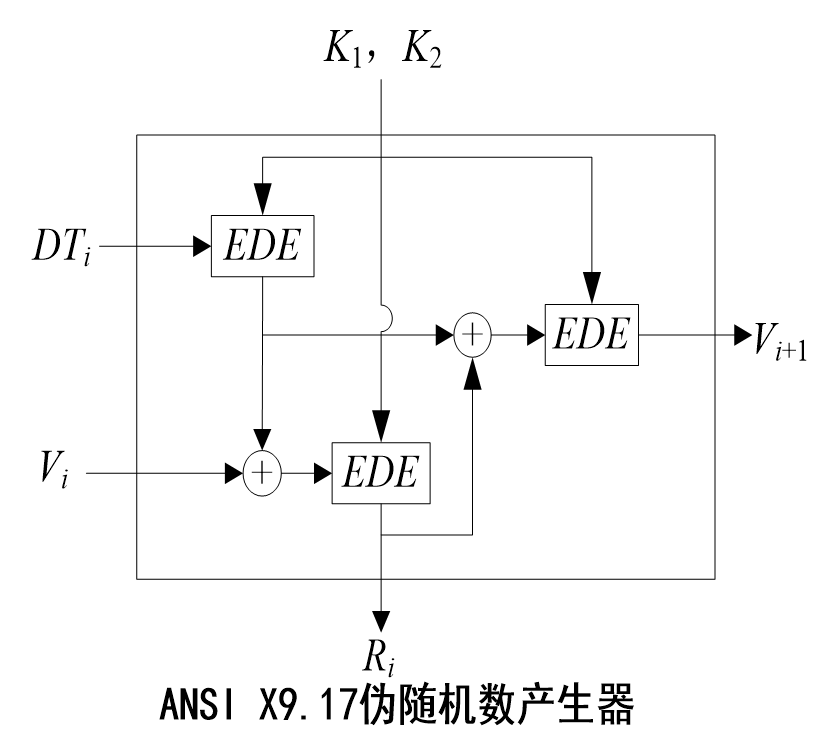
ANSI X9.17 伪随机数产生器
- 密码强度最高的伪随机数产生器之一
- 组成部分
- 输入: 表示当前的日期和时间 ;Vi是产生第 个随机数时的种子
- 密钥:
- 输出:一个64比特的伪随机数 ,一个64比特的新种子 ,
流密码
流密码的概念
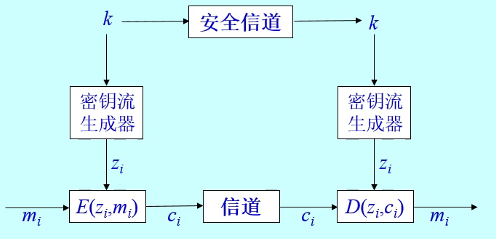
加密算法:
解密算法:
-
在使用的流密码中,加密变换通常采用二元加法运算。即:
-
由于一次一密的传输和存储麻烦,所以可行改进的办法是,用一个较小的密钥伪随机产生一个密钥流(从无条件安全变成了计算上安全)
- 密钥发生器:驱动部分(统计特性好序列)和非线性组合部分(密码学特性好序列)
流密码分类
- 根据 与明文信息的关系,流密码可以分为同步流密码和自同步流密码两类
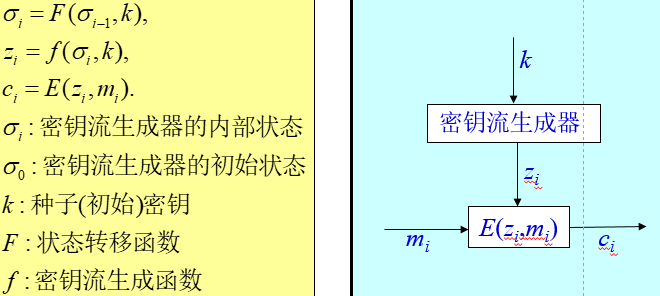
同步流密码
-
独立于明文字符的叫做同步流密码。
-
对明文而言,同步流密码的加密变换无记忆;解密要求密钥流与加密密钥严格同步
-
特性
-
只要通信双方的密钥序列产生器具有相同的“种子序列”和相同的“初始状态”,就能产生相同的密钥序列.
-
容易检测插入、删除、重播等主动攻击.
-
没有差错传播.
-
自同步流密码
- 与明文 有关,称为自同步流密码
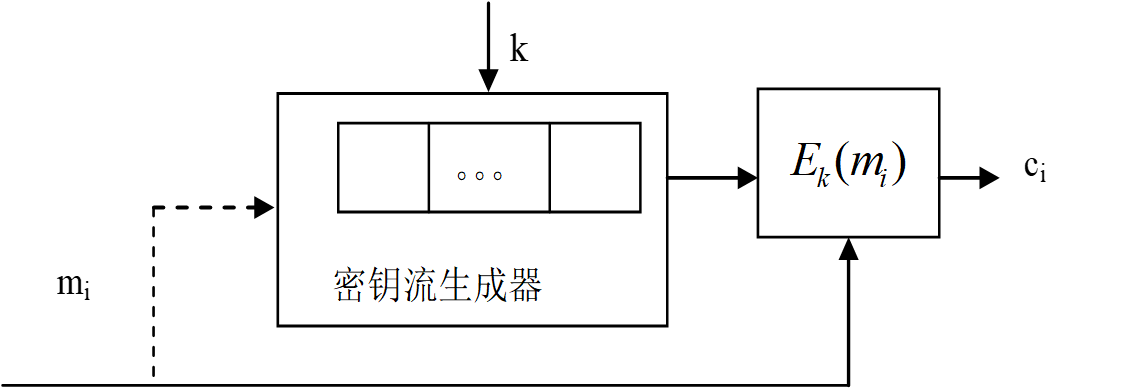
-
特性
-
密钥流生成器是一种有记忆变换器,密钥流与明文符号有关:
- i 时刻的密文不仅取决于 i 时刻的明文,且与 i 时刻之前的 l 个明文符号有关;
-
具有有限的差错传播;
-
具有自同步能力;
-
把明文每个字符扩散在密文多个字符中,强化了抗统计分析的能力
-
线性移位寄存器
-
反馈移存器是序列密码设计中常用乱源。
-
目的:以种子密钥为序列的初态,按照确定的递推关系,产生一个周期长、线性复杂度高、统计特性好的初始乱源,然后利用非线性函数、有记忆变换等密码变换,最终产生抗破译能力强的乱数序列。
-
线性移位寄存器序列是构造密钥流序列的基础。
反馈移位寄存器
- 一个反馈移位寄存器由两部分组成:移位寄存器和反馈函数,其抽象的简单逻辑框图如下图所示。
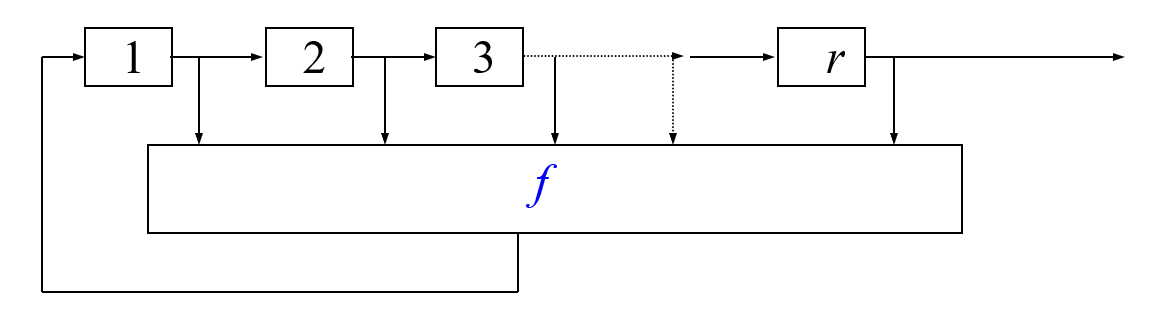
-
称这一函数为该组合门电路的反馈逻辑函数,表示为:
,函数 是一个含有 个逻辑变元的布尔函数
-
若反馈移存器的反馈逻辑函数是线性函数,则称该反馈移存器为线性反馈移存器,否则称为非线性反馈移存器
-
如果反馈函数 是 个变量的线性函数:
则称为线性反馈移位寄存器(LFSR: linear feedback shift register)。
输出的序列称为线性反馈移位寄存器序列, 记为LFSR序列。
-
递推关系式:
-
如果 ,则称LFSR是退化的;否则称 LFSR 是非退化的。
-
把多项式:
称为 LFSR 的特征多项式(characteristic polynomial), 或级连多项式或生成多项式
-
-
-
反馈移存器工作原理
-
反馈移存器的功能完全由其反馈逻辑函数来决定
-
移存器受时钟脉冲控制,在某一时刻各级都有一个确定的值,把此时刻各级的值称为移存器的一个内部状态
-
-
序列和周期
-
对于序列 ,若存在整数 使得对任意整数 有 成立,称满足该式的最小正整数 为序列的周期。
-
最长周期: ,能达到最长周期的线性移存器序列称为 m 序列
-
-
线性移存器表示方法
- 一个 级线性移存器的线性递推式表示为:
流密码算法
RC4 算法
-
RC4是由Rivest于1987年开发的一种序列密码,它已被广泛应用于Windows、 Lotus Notes和其它软件,还被用于安全套接字(SSL)和无线通信系统等;
-
RC4优点是算法简单、高效,特别适于软件实现,加密速度比DES大约快10倍。
-
RC4可以支持不同密钥长度,美国政府特别限定,用于出口的RC4的密钥长度不得超过40位。
-
算法步骤
-
RC4 使用了一个 28 字节大小的非线性数据表(简称 S表),S 表的值 是数字 0 到 255 的一个排列。对 S 表进行非线性变换,得到密钥流。
-
RC4对S表的初始化算法(两个计数器 I 和 J, I =0 , J=0)
-
对S表进行线性填充:;
-
用密钥填充另一个 256 字节的数组 K,如果密钥长度小于256字节,则依次重复填充,直至填满这个数组中:;
-
对于 I=0 到 255 重复以下步骤:
(1) ;
(2) 交换 和 。
-
-
将 和明文进行 xor 运算,得到密文
-
公钥密码原理
为什么引入公钥密码体制?
对称密码体制的问题
- 密钥分配问题
- 密钥传输问题:传输信道安全性并不理想
- 密钥管理问题:需管理的密钥 ,加入一个用户,产生 个密钥
- 没有签名功能
※ 根源:对称密码的加密密钥与解密密钥相同
解决方法
- 将密钥分为加密密钥和解密密钥
- 加密密钥公开,解密密钥保密
| 问题描述 | 公钥密码体制完美解决 |
|---|---|
| 密钥分配 | 无需密钥的秘密分配。 |
| 密钥管理 | 每个用户需秘密保存1个私钥;网络中需要管理的密钥数目为n对。新用户加入时,系统只需产生1对公私钥对。 |
| 签名功能 | 提供了数字签名功能。 |
什么是公钥密码体制?
公钥密码体制的原理
- 公钥体制:每个用户都有一对选定的密钥(公钥k1;私钥k2),公开的密钥k1可以像电话号码一样进行注册公布
- 主要特点:
- 加密和解密能力分开
- 多个用户加密的消息只能由一个用户解读(用于公共网络中实现保密通信)
- 只能由一个用户加密消息而使多个用户可以解读(可用于认证系统中对消息进行数字签字)
- 无需事先分配密钥
公钥密码体制概述
- 公钥密码体制是密码学研究的一个具有里程碑意义的重要事件。
- 公钥密码技术又称为双钥密码或非对称密码技术。
- 1976年由Diffie和Hellman在其《密码学新方向》一文中首次提出公钥密码思想
公钥密码体制组成
- 公钥密码体制有6个组成部分:
- 明文:算法的输入;
- 密文:算法的输出;
- 公钥和私钥:算法的输入;
- 加密算法:对明文进行各种变换;
- 解密算法:接收密文和相应的密钥,并产生原始的明文。
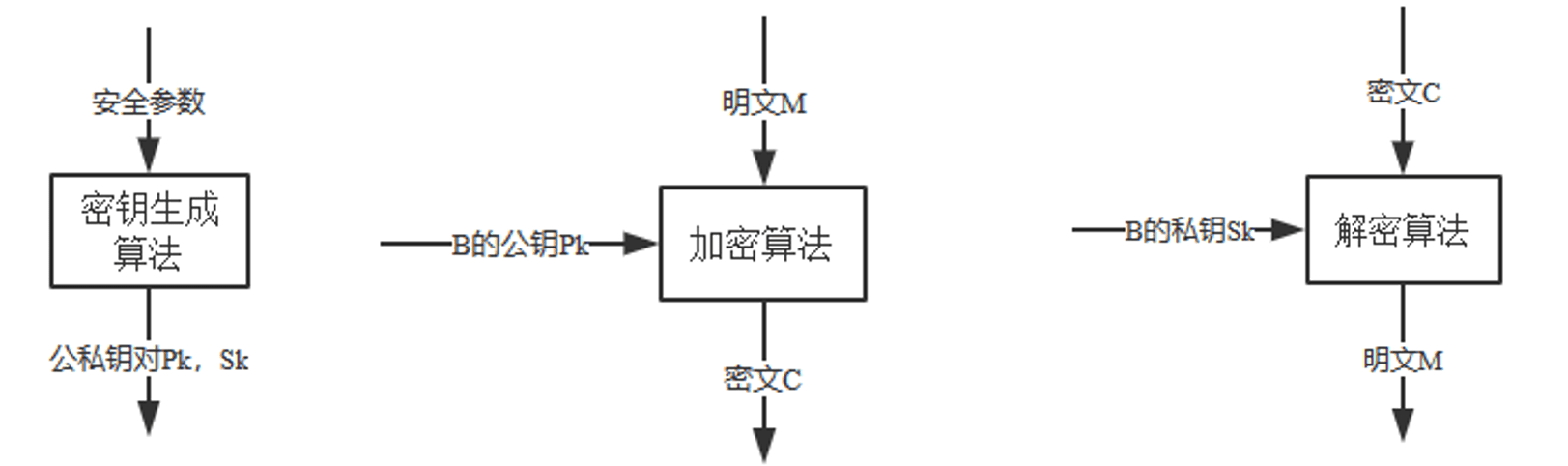
公钥密码体制功能
- 公钥密码体制的主要特点是将加密和解密能力分开,因而可以实现多个用户加密的信息只能由一个用户解读,或由一个用户加密的信息而多个用户可以解读。
- 前者可以用于公共网络中实现通信保密,而后者可以用于实现对用户的认证。
公钥体制加、解密安全保障
用公钥密码实现保密
- 用户 B 拥有自己的密钥对
- 公钥 公开,私钥 保密
- (公钥加密)
- (私钥解密)
从公开钥 和密文 要推出明文 或解密钥 计算上不可行。
由于任一用户都可用用户 B 的公开钥 向他发送机密消息,因而密文 不具有认证性。
用公钥密码实现认证
- 条件: 两个密钥中任何一个都可以用作加密而另一个用作解密
- 认证:
(A用私钥签名)
(用A的公钥认证)
由于 是保密的,其他人都不可能伪造密文 ,可用 A 的公开钥解密时得到有意义的消息 。因此可以验证消息 来自 A 而不是其他人,而实现了对 A 所发消息的认证。
公钥保密和认证体制
-
认证+保密:
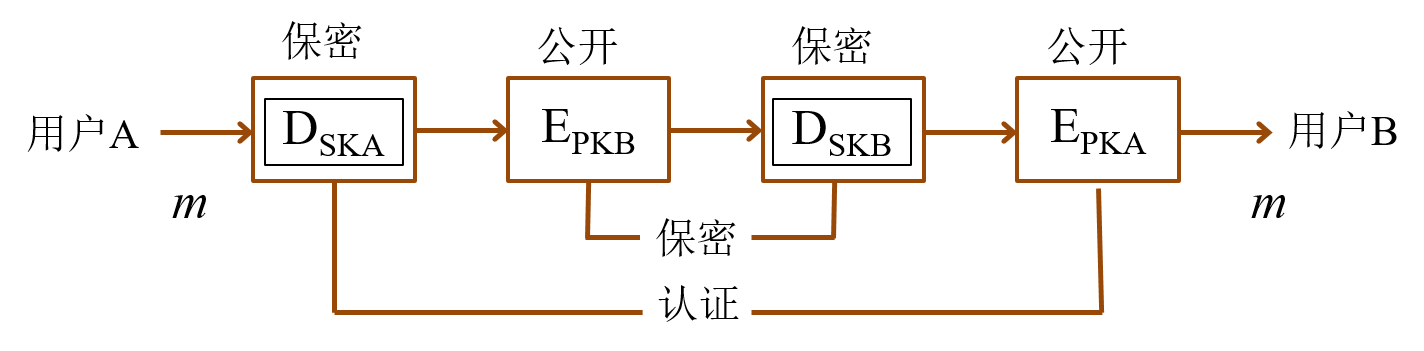
公钥密钥的应用范围
| 算法 | 加/解密 | 数字签名 | 密钥交换 |
|---|---|---|---|
| RSA | 是 | 是 | 是 |
| Dieffie-Hellman | 否 | 否 | 是 |
| DSS | 否 | 是 | 否 |
公钥密码应满足的要求
-
公钥密码应满足的要求
-
涉及到各方:发送方、接收方、攻击者
-
涉及到数据:公钥、私钥、明文、密文
-
-
公钥算法的条件:
- 对于接收者:产生一对密钥是计算可行的
- 对于发送者:已知公钥和明文,产生密文是计算可行的
- 对于接收者:接收方利用私钥来解密密文是计算可行的
- 对于攻击者:利用公钥来推断私钥是计算不可行的
- 对于攻击者:已知公钥和密文,恢复明文是计算不可行的

如何设计公钥密码体制?
第一步转化:设计公钥密码体制变成了寻找陷门单向函数
- 单向陷门函数是满足下列条件的函数 :
(1) 计算 是容易的;
(2) 给定 , 计算 使 是困难的;
(3) 存在 ,已知 时,对给定的任何 ,若相应的 存在,则计算 使 是容易的。
仅满足(1)、(2)两条的称为单向函数,单向函数不能用于加密
第(3)条称为陷门性, 称为陷门信息。
第二步转化:如何在求解NP完全问题中设置合理“后门”
由于利用目前现有的技术无法在多项式时间里对NP完全问题进行求解,公钥密码思想的首创者 Diffie 和 Hellmen 在其研究中指出:
计算复杂性可以被用作设计加密算法的基础,NP完全问题则是一个理想的解决途径!
-
信息通过编码被加密在一个 NP 完全问题之中,使得要破译这种密码以普通的方法就要解这个 NP 完全问题;
若使用解密密钥,就可能有捷径求解。- 为构造这样的密码,陷门信息必须被嵌在一个计算困难问题中。
-
并非所有困难问题都可用于设计公钥密码系统。通过检验,已找到的可提供单向函数的数学难题包括:
- 整数分解问题(简称IFP)
- 有限域离散对数问题(简称DLP)
- 椭圆曲线离散对数问题(简称ECDLP)
-
基本思想:
- 选择一个容易求解的子集和问题实例,伪装成一个很难求解的一般子集和问题实例;
- 容易求解的子集和问题实例用作私钥;
- 不易求解的子集和问题实例用作公钥。
※: 举例:如何使用背包问题构造背包密码体制
已知一长度为 B 的背包,及长度分别为 的 n 个物品。假定这些物品的半径和背包相同,若从这 n 个物品中选出若干个正好装满这个背包。现在反过来问:究竟是哪些物品?
-
等价于求 ,使其满足: ,其中 和 都是整数。
-
背包问题属于NP完备类(NP问题中难度最大的一类),对这类问题没有有效算法。但是,如果序列 是超递增序列,则背包问题有多项式解法。
-
对于背包问题进行如下定义:
背包向量:,
选择向量:长度为 n 的比特串。
超递增背包向量: 超递增序列。
已知背包向量和选择向量,可得到背包的容积:(背包向量,选择向量)=容积
已知容积和背包向量,很难求出选择向量;
已知超递增背包向量和容积,易求选择向量:- 对应公钥密码体制,设置:
明文 为选择向量,密文 为容积,公钥 为背包向量,私钥 为超递增背包向量。
- 对应公钥密码体制,设置:
RSA 公钥密码体制
算法背景
-
该算法的数学基础是初等数论中的Euler(欧拉)定理,并建立在大整数因子分解的困难性之上,目前还不存在一般性的有效解决算法。
-
大整数的分解问题可以被表述:已知整数 是两个素数的积,即 。求解 的值。
-
与 互素,则由 Euler 定理得:
即
算法描述
密钥产生算法
- 随机生成两个不同且大小相近的大素数 和 。
- 计算 ,,其中 是 的欧拉函数值。
- 选一整数 ,满足 ,且 。
- 计算 ,满足 ,即 是 在模 下的乘法逆元,因 与 互素,由模运算可知,它的乘法逆元一定存在。
- 以 为公开钥, 为秘密钥。
密钥产生细节
-
选取大素数的方法:随机产生一个大整数,利用素性检测算法判定该整数是否为素数
-
以往素检测的算法都是概率性的,即存在一定的错误概率;
-
2003年,印度人发表文章 “Primes is in P”,证明了素判定问题是一个多项式时间问题。
加解密
加密
- 获得 A 的可信公钥 ;
- 将明文 比特串分组,使得每个分组对应的十进制数小于 ,即分组的长度小于 ;
- 对每组明文分组,作加密运算:
- 将密文 C 发送给 A 。
解密
- 对密文分组的解密运算为:
加解密细节
- 实际应用中,在RSA算法的加密与解密过程中,被加密的是经过分组的数据段。各数据段的长度相等,并且小于比 小的 2 的最大次幂。
- 当需要加密固定长度的数据段时,可以在长度不足的各数据段的左边位上填充 0 作为补充。
解密过程针对的也是被加密的这些数据段。因此,经解密得到的依然是经过分组的数据段。将这些数据段依次连接便能得到被传输的消息原文。
- 当需要加密固定长度的数据段时,可以在长度不足的各数据段的左边位上填充 0 作为补充。
RSA 中的计算问题
计算技巧
RSA 加密
- 模指数运算的快速算法
RSA 解密
-
加密很快,指数小;解密比较慢,指数较大
- 利用中国剩余定理CRT,加快计算速度。
CRT 对RSA解密算法生成两个解密方程(利用 )
即:
解方程组:
利用CRT:
具有唯一解:
密钥生成
- Miller Rabin 素数判定测试
RSA 安全性分析
- 已知 , 和 ,产生 是计算可行的——加密函数
- 对于攻击者,已知 , 和 ,要恢复 是计算不可行的——解密函数
- 存在能解密的陷门——解密私钥 。
理解求d的困难性
解密函数
1)Attacker得到一对 ,试图还原 ,以便以后的解密,这就是离散对数问题。也就是找到 ,满足 是很难的。
2)Attacker知道公钥 ,通过公钥去得到私钥是很难的。
→ 求 → 求素因子 , → 大数因子分解的困难性
RSA 的攻击
-
穷举攻击:穷举所有可能的私钥
-
数学攻击:
- 因式分解攻击
- 参数的选取不当造成的攻击
- 选择密文攻击
- 共模攻击
- Hastad对广播信息的攻击(小e攻击)
- 小指数攻击(可以用连分数方法)
- 加密及签名攻击
- 鲁棒性攻击
- 数学性的鲁棒性攻击
-
计时攻击
-
用定时攻击方法分解出私钥
-
基于密码分析的错误攻击(基于脆弱性的中国剩余定理)
-
对于已知部分密钥位的攻击
RSA密码体制的实现要求
对 n,p,q,e 的要求
若使 RSA 安全, 与 必为足够大的素数,使分析者没有办法在多项式时间内将 分解出来。建议选择:
-
和 大约是 100 位的十进制素数。
-
模 的长度要求至少是 512 比特。
- EDI(电子数据交换)国际标准使用的 RSA 算法中规定 的长度为 512 至 1024 比特位之间,但必须是 128 的倍数。
- 国际数字签名标准ISO/IEC 9796中规定 的长度为 512 比特位。
- SET(secure electronic transaction) 协议中要求 CA 采用 2048 位的密钥,其它实体使用 1024 位的密钥
-
为了抵抗现有的整数分解算法,对RSA模 的素因子 和 还有如下要求:
- 很大,通常 和 的长度相同;
- 为强素数。
- 一个素数 是强素数需要满足以下三个条件:
- 有大的素数因子,称为 ;
- 也有大的素数因子;
- 仍然有大的素数因子。
- 原因:
- 第一个条件的原因是存在 分解算法,这一算法只在模 存在一个素数因子 满足 平滑时有效;
- 第二个条件的原因是存在 分解算法,这一算法只在模 存在一个素数因子 满足 平滑时有效;
- 第三个条件的原因为了保证循环攻击无效。
- 一个素数 是强素数需要满足以下三个条件:
RSA 的速度
- 在RSA的软件实现上,RSA 大约比 DES 慢 100 倍。
- 在RSA的硬件实现上,粗略地说,RSA 比 DES 慢 1500 倍。
- 为了提高加密速度,通常取e为特定的小整数,如 EDI 国际标准中规定 ,ISO/IEC9796中 甚至允许取 。这时加密速度一般比解密速度快 10 倍以上。
- 虽然因为计算机技术的改进,RSA 的速度不断改变,但其永远无法达到对称密钥算法的运行速度。
- 具体应用中将 RSA 算法更多地用于密钥的安全传输过程,而在针对具体传输信息的加密与解密中依靠对称密钥算法,这样便能够增进密码系统的运行速度。
RSA算法的优缺点
优点
-
是第一个能同时用于加密和数字签名的算法,也易于理解和操作.
-
特别符合计算机网络环境。
-
对于网上的大量用户,可以将加密密钥用电话簿的方式印出。
缺点
- 产生密钥很麻烦,受到素数产生技术的限制,因而难以做到一次一密;
- 分组长度太大,为保证安全性,n 至少也要 600 位以上,使运算代价很高,尤其是速度较慢,较对称密码算法慢几个数量级;且随着大数分解技术的发展,这个长度还在增加,不利于数据格式的标准化。
椭圆曲线密码体制 ECC
椭圆曲线密码简介
-
椭圆曲线密码是基于椭圆曲线数学的一种公钥密码的方法
-
椭圆曲线在密码学中的使用在 1985 年由 Neal Koblitz 和 Victor Miller 分别独立提出
-
与传统的基于大质数因子分解困难性的加密方法不同,ECC通过椭圆曲线方程式的性质产生密钥。
-
ECC被广泛认为是在给定密钥长度的情况下,最强大的非对称算法,因此在对带宽要求十分紧的连接中会十分有用。
-
ECC的主要优势:在某些情况下它比其他的方法使用更小的密钥提供相当的或更高等级的安全
- 速度快、密钥短
-
椭圆曲线密码学的许多形式有稍微的不同,所有都依赖于被广泛承认的解决椭圆曲线离散对数问题的困难性上,对应有限域上椭圆曲线的群。
-
对椭圆曲线来说最流行的有限域是
- 以素数为模的整数域 ,通常在通用处理器上更为有效;
- 特征为2的伽罗华域 ,在专门的硬件实现上计算更为有效。
椭圆曲线的基本概念
-
无穷远点
- 定义平行线相交于无穷远点 ,使平面上所有直线都统一为有唯一的交点
- 性质:
- 一条直线只有一个无穷远点;一对平行线有公共的无穷远点
- 任何两条不平行的直线有不同的无穷远点(否则会造成有两个交点)
- 平面上全体无穷远点构成一条无穷远直线
-
射影平面
- 平面上全体无穷远点与全体平常点构成射影平面
- 对普通平面上点 ,令 ,则投影为射影平面上的点
- 例如:点 可投影为 ,可为 等
- 对普通平面上的直线 ,同样变换,得到对应于射影平面上的直线为
- 无穷远点的坐标为
-
椭圆曲线
-
一条椭圆曲线是在射影平面上满足威尔斯特拉斯方程(Weierstrass)所有点的集合:
-
椭圆曲线方程是一个齐次方程,无穷远点
-
椭圆曲线普通方程:
-
曲线上的每个点都必须是非奇异的(光滑的),偏导数 不同为0
-
椭圆曲线并非椭圆,称为椭圆曲线是因为它的曲线方程与计算椭圆周长的方程类似。
-
-
椭圆曲线普通方程
-
椭圆曲线普通方程:
-
常见形式为:,其中
-
曲线关于 对称
-
平常点 斜率
-
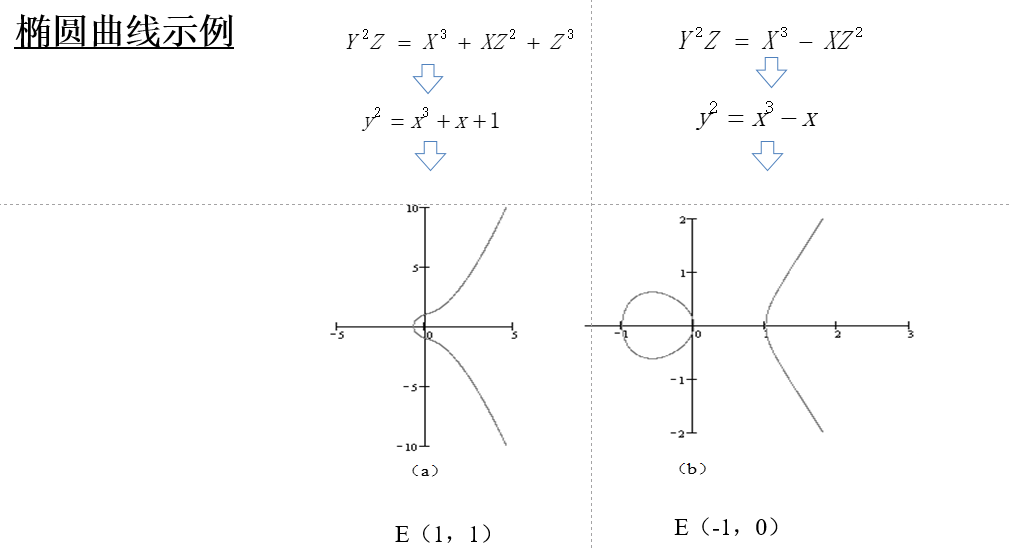
实域R上的椭圆曲线
-
椭圆曲线表示为平面上通常曲线上的点,外加无穷远点 。
-
设 为一条直线。因为 E 的方程是三次的,所以 L 可与 E 在 上恰有三个交点,记为P、Q、R(如果 L 与 E 相切,那么 P、Q、R 可以不相异)。
椭圆曲线上的加法运算
-
如果其上的 3 个点位于同一直线上,那么它们的和为 。进一步可如下定义椭圆曲线上的加法律
- 为加法单位元,即对椭圆曲线上任一点 ,有
- 设 是椭圆曲线上的一点,它的加法逆元定义为
- 设 和 是椭圆曲线上 x 坐标不同的两点, 的定义如下: 画一条通过 的直线与椭圆曲线交于 ,由 得 。
-
点加公式
则:
-
数乘定义为重复相加
有限域上的椭圆曲线
上的椭圆曲线
-
定义:
满足上式的所有整数对和无穷远点组成的集合
-
点加公式
则:
\lambda=\begin{cases}\frac{y_Q-y_P}{x_Q-x_P}\bmod p && P\neq Q \\\frac{3x_P^2+a}{2y_P}\bmod p &&P=Q \end{cases}\end{aligned}
上的椭圆曲线
-
-
点加公式
-
则:
-
则:
-
椭圆曲线密码体制
- 椭圆曲线密码体制依据是定义在椭圆曲线点群上的离散对数问题的难解性
- ECC Diffie-Hellman 密钥交换

用椭圆曲线实现ElGamal密码体制
-
密钥生成过程
- 用户 A 选择一条椭圆曲线 ,取椭圆曲线上的一个生成元
- 用户 A 选择一个正整数 作为秘密密钥,并生成公开密钥
- 用户 A 把 、 和 传给用户 B
-
加密过程
Alice要发送消息m给Bob,Alice执行:
- 查找 Bob 的公钥
- 将 m 表示成一个域元素
- 在区间 内选取一个随机数
- 依据 Bob 的公钥计算点 ( 个 相加)
- 计算点 ,如果 ,则回到第3步
- 计算
- 传送加密数据 给 Bob
-
解密过程
Bob收到Alice的密文 后,执行
-
使用私钥 ,计算点 ,再计算 中
-
通过计算 ,恢复出明文数据
-
椭圆曲线密码体制的优点
- 安全性高,椭圆曲线密码体制比基于有限域上的离散对数问题的公钥体制更安全
- 密钥量小
- 灵活性好:在密钥长度相等的情况下,RSA和ECC的速度相当;但是在相同的安全强度要求下,ECC可以使用较少的位数就可以
- 速度快:在密钥长度相等的情况下,RSA和ECC的速度相当;但是在相同的安全强度要求下,ECC可以使用较少的位数就可以
其他密码体制
Rabin 密码体制
-
Rabin密码体制有两个特点:
-
不以一一对应的单向陷门函数为基础,对同一密文,可能有两个以上对应的明文
-
破译该体制与分解大整数是等价的
-
-
密钥产生算法
- 随机选择两个大素数 ,满足 ,即这两个素数形式为 ;计算 。以 作为公钥, 作为密钥。
-
加密
是明文分组, 是对应的密文分组。
-
解密
解密即为求解 ,由 CRT知该方程等价于解方程组:
Diffine-Hellman密钥交换
-
Diffie-Hellman算法是第一个公开密钥算法,发明于1976年。Diffie-Hellman算法能够用于密钥分配,但不能用于加密或解密信息
-
Diffie-Hellman 算法的安全性依赖于有限域上计算离散对数非常困难
-
步骤
如果A和B想在不安全信道交换密钥,可采用如下步骤:
- A 和 B 协商一个大素数 及 的本原根 , 和 公开
- A 秘密产生随机数 ,计算 ,发送 给 B
- B 秘密产生随机数 ,计算 ,发送 给A
- A 计算
- B计算
-
中间人攻击
Diffie-Hellman密钥交换容易遭受中间人攻击:
-
A 发送公开值 给 B,攻击者 C 截获,并把自己产生的公开值发送给 B
-
B发送公开值给 A,C 截获,把自己的公开值 发送给 A
-
A 和 C 计算出二人的共享密钥
-
B 和 C 计算出另外一对共享密钥
- 造成中间人攻击的原因是 Diffie-Hellman 密钥交换不认证对方
-
ElGamal密码体制
-
ElGamal 算法在密码协议中有许多实际应用,安全性基于求解离散对数问题的困难性
-
密钥生成算法
-
选取一个足够大的素数 ,使求解离散对数问题在 上是困难的;
-
在 上选择一个本原元
-
随机选取整数 ,并计算 ;
公钥为:;私钥为:
-
-
加密:Alice 取一个秘密随机数 ,对明文 加密
其中, -
解密:Bob 计算
数字签名
-
数字签名(digital signature),也称电子签名,是对电子文档利用电子手段进行签名;
-
电子签名必须至少具备手写签名的两个性质,即可验证性与不可伪造性。
-
主要功能:确认数据单元来源和数据单元的完整性
- 确认信息是由签名者发送的
- 确认消息自签名后到收到为止,未被修改过
- 签名者无法否认签名是由自己发送的
-
数字签名必须具有下列特征:
-
能验证签名者、签名日期和时间;
-
能认证被签的消息内容;
-
能由第三方仲裁,以解决争执。
简单说,数字签名是个加密的过程,数字签名的验证是一个解密的过程。
-
签名方案
一个签名方案是一个 5 元组 ,满足如下的条件:
- 是一个可能消息的有限集;
- 是一个可能签名的有限集;
- 密钥空间 是一个可能密钥的有限集;
- 对每一个 ,都对应一个签名算法 和验证算法 。
- 每一个 和 是一个对每一个消息 和每一个签名 满足下列方程的函数:
- 对每一个 ,函数 和 都是多项式时间可计算的函数。 是一个公开函数, 称作公钥;而 是一个秘密函数, 称作私钥,由用户秘密地保存。
数字签名的安全性
-
攻击者能力
- 唯密钥攻击:攻击者C只拥有签名者A的公钥。
- 消息攻击
- 已知消息攻击:C拥有一些消息与相应的签名.
- 一般选择消息攻击:在攻击A的签名方案之前,C首先选择一些消息,而无需知道A的公钥。C对于选择的消息从A处获得合法签名。
- 定向选择消息攻击:攻击者在掌握A的公钥之后,在签名生成之前选择消息。
- 适应性选择消息攻击:允许C将A作为“oracle”进行轮询。
-
敌手的目标:伪造签名
- 完全攻破:C找到A的私钥d.
- 通用伪造:C掌握一个有效的签名算法,使得对于任意消息都能够等价地构造出合法签名。
- 选择伪造:C对于所选特定消息能够为找出合法签名。
- 存在性伪造:C至少可伪造出一个消息的合法签名,但C不能控制该消息的选择。这种伪造对于A的危害最低。
数字签名的设计目标
- 签名必须是与消息相关的二进制位串;
- 签名必须使用发送方某些独有的信息,以防伪造和否认;
- 产生数字签名比较容易;
- 识别和验证签名比较容易;
- 伪造数字签名计算上不可行,无论攻击者采用何种方法(利用数字签名伪造报文,或者对报文伪造数字签名)。
- 保存数字签名的副本是可行的。
数字签名的解决方案
-
直接数字签名方案
- 技术上仅涉及到通信双方
- 发送方可以声称自己的私钥丢失或被盗用,而否认其发送过某个报文
- 改进:每个签名报文中包含一个时间戳
-
基于仲裁的数字签名方案
- 通过引入仲裁来解决直接签名方案中的问题
- 基本工作方式
- 每个从X发往Y的签名报文首先被送给仲裁者 A
- A 检验该报文及其签名的出处和内容,然后对报文注明日期,并附加上一个“仲裁证实”的标记发给 Y
常见的数字签名算法
Elgamal 数字签名
- ElGamal 签名方案由 T.ElGamal 于1985年提出,其安全性主要基于有限域上离散对数问题的难解性。
- 是 ElGamal 公钥密码体制的直接应用。
- 一般 ElGamal 签名方案
- 系统初始化
设 是一大素数, 是 的一个生成元,A执行如下:- 生成随机整数 ,;
- 计算 ;
- A 的私钥是 ,A的公钥是
- 签名算法
对于待签消息 ,用户 A 计算:- Hash 值 ;
- 选择随机数 ,计算 ; 计算
- 签名为
- 验证算法
- 任意接收方验证如下:
- 计算
- 计算
- 如果 ,则签名合法
- 任意接收方验证如下:
- 系统初始化
Schnorr数字签名
-
密钥生成算法
- 选择素数 ,使得 是 的素因子
- 选择整数 ,使得 。值 和 构成全局公钥参数,在用户组内的每个用户都可取此值
- 选择随机整数 ,,作为用户的私钥
- 计算 ,作为用户公钥
-
签名算法
-
对于待签消息 ,选择随机数 ,计算 (与待签名消息无关,可以预处理)
-
计算
-
计算
-
发送签名对 。
-
-
验证算法
- 收方收到消息 和数字签名
- 计算
- 验证是否
※ : 表示级联
Schnorr数字签名方案的安全性分析
-
EIGAMAL系统中 为 中的本原元,而 Schnorr 系统中则不是。
- 从安全角度看,ElGamal 安全性较高,这是因为本原元的阶为 ,而 Schnorr 系统中 g 的阶为 ,在此阶下,基于LP的体制是否安全有待进一步研究。
-
Schnorr 系统的签名文较短,e 的长度由函数 h 决定。
数字签名标准DSA算法
- DSA的安全性主要依赖于有限域上离散对数问题的难解性,是 ElGamal 签名算法的变种
- 步骤
※:对每一个报文需要选择不同的

RSA和相关签名方案
RSA签名方案
-
初始化阶段
实体 A 执行如下操作:- 随机产生大小相近的两个不同大素数 和
- 计算 ,其欧拉函数值 ;
- 随机选一整数 , ,满足 ;
- 利用扩展的欧几里德算法,计算惟一的整数 , ,满足 ;
- 公钥为 ;私钥为 。( , 不再需要,可以销毁)
-
签名生成算法
- 计算取值在区间 内的整数
- 计算
- A 对 的签名为
-
签名验证算法
为验证A的签名 且恢复消息 ,B执行如下操作:
- 获得A的可信公钥
- 计算
- 验证 ;否则拒绝接受签名
- 4.恢复
-
扩展:带消息恢复的 RSA 数字签名、带附录的 RSA 数字签名
Rabin公钥签名方案
- 密钥生成:每个实体生成各自的公钥和相应私钥。
实体A执行如下操作:- 随机产生两个不同的大素数 和
- 计算
- A 的公钥是 ,私钥是
- 签名生成:实体 A 签署消息 m
- 计算
- 计算 的一个平方根
- A 对 的签名是
- 验证:为验证签名s且恢复消息m,B执行如下操作
- 获得公钥
- 计算
- 验证 ;否则拒绝接受签名
- 恢复
具有特殊功能的数字签名
-
盲签名
- 需要盲签名的情形:当 Bob 想让 Alice 对一个文档签名,但他又不想让 Alice 知道这个文档的内容,且 Alice 在签署文档后不能将这次签名追踪到 Bob 时需要盲签名.
- 盲签名的步骤:
- Bob 对要签署的消息进行盲化
- Alice 对盲化过的消息进行签名
- Bob 进行脱盲恢复原来消息的签名
- 应用:电子选举
-
群签名
-
群签名具有三个性质:
- 群里的任何人都可以群的名义对文档签名;
- 签名的接受者可以验证签名是这个群的合法签名,但不知道它是群中哪个成员所为,
- 如遇争执,一个可信机构能识别出那个签名者
-
一个群签名方案
-
部门经理(相当于可信机构)选定本部门(群)的公钥方案,比如RSA,然后为每个成员选定若干私钥并告知他,再将群里每个成员的公钥随机排列成一表并公布。
-
每个成员在打印的时候,随机选择一个私钥进行签名,每个私钥只能使用一次,否则验证者可将这些签名联系起来。
-
签名接受者收到一个群签名,使用这个群的公钥列表一个个验证,只要有一个公钥通过验证,则是合法签名,否则非法。
-
发生争执,部门经理能找出具体的签名者。
-
-
-
代理签名
- 现实中,利用印章签名可实现代理,即印章的拥有者将印章给别人。当自己有事的时候,这个人就可以对文件盖章相当于以他的名义对文件签名。
- 所谓代理签名是指:在一个代理签名方案中,一个代理签名者可代表原始签名者生成有效的签名。
-
门限数字签名
- 门限数字签名体制是面向组织或团体的签名体制,能解决如何由集体而非个人进行数字签名的问题,是数字签名体制研究的重要分支。
-
批验证协议
- 安全的批验证协议需满足如下的条件:
- 签名者在签名过程中一次产生多个消息的签名;
- 多个签名的有效性由签名验证者一次验证完成;
- 多个有效的签名一定满足批验证协议中的批验证原则;
- 在批验证协议中有效的多个签名一定是有效的签名。
- 安全的批验证协议需满足如下的条件:
密码学 Hash 函数
Hash 函数的定义
-
Hash函数也叫散列函数、哈希函数、杂凑函数
-
哈希函数是一公开函数,通常记为 ,用于将任意长的消息 映射为较短的、固定长度的一个值,记为
-
对于大的输入集合使用该函数,产生的输出结果均匀地分布且看起来随机
-
Hash函数首要目标是保证数据的完整性,对于 任何一位或几位的改变都将极大可能改变其hash码
-
从密码角度看,散列函数可看作是一种单向密码体制
-
找到两个不同的数据块对应相同的Hash值在计算上不可行
Hash 函数的应用
消息认证
-
是用来验证消息完整性的一种机制或服务
-
确保收到的数据确实和发送时的一样(即没有修改、插入、删除或重放),且发送方声称的身份真实有效
-
当哈希函数用于提供消息认证功能时,Hash函数值通常称为消息摘要
-
一般通过使用消息认证码(MAC)实现,即带密钥的Hash函数
广泛应用于文件传输(如网络文件下载)
-
利用 Hash 函数检查数据完整性
- 在该例中,Hash 函数必须得到保护,否则,Darth 拦截了该消息后,篡改其中的数据,然后重新计算 Hash 值并附在后面。Bob 无法发现消息被篡改了。

-
几种可行的改进方法
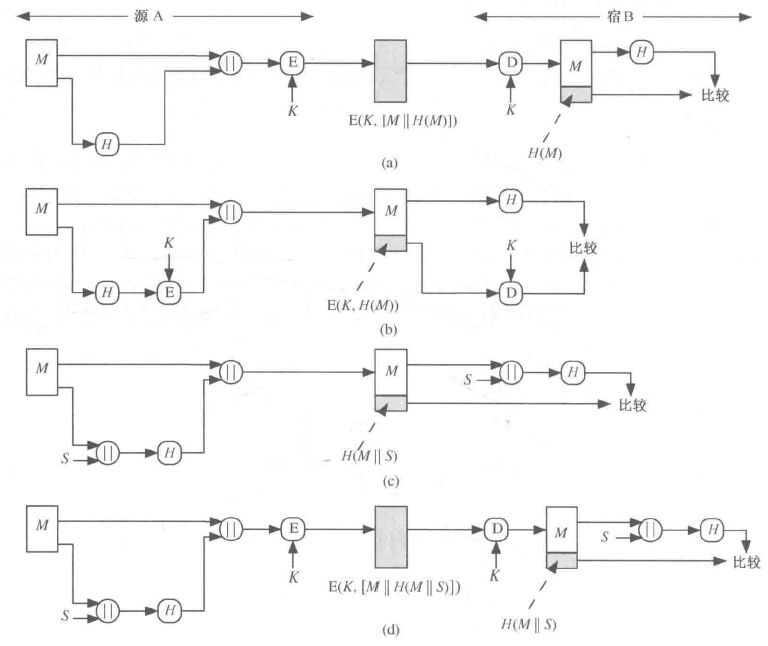
(a)消息与 Hash 值链接后用单钥加密算法加密
- 有保密性
(b)用单钥加密算法仅对 Hash 值加密
- 无保密性
(c)使用共享秘密值 S
- 无保密性,但是敌手由于不知道 S,无法产生假消息
(d)在(c)的基础上,对整个消息和 Hash 值加密
- 有保密性
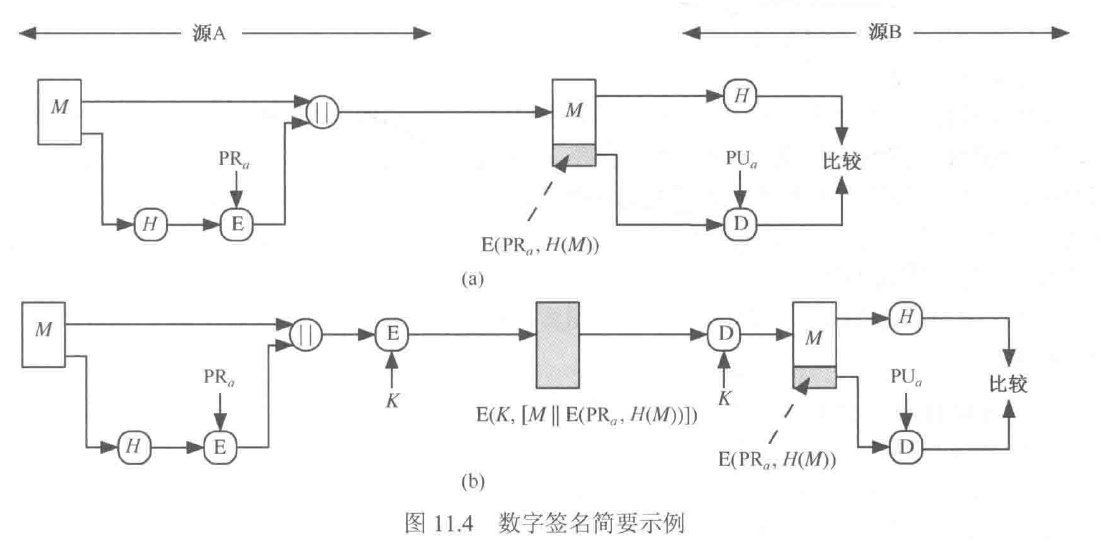
数字签名
-
使用用户的私钥加密消息的Hash值,其它任何知道该用户公钥的人通过数字签名验证消息的完整性。
-
攻击者要想篡改消息,则需要知道用户私钥。
-
优点:
- 提高签名速度——可以预处理消息的Hash值
- 可以不泄露签名所对应的消息
-
利用 Hash 函数进行数字签名
其他应用
- 产生单向口令文件:
如操作系统存储口令的Hash值而不是口令本身,大多数操作系统都采用了这种口令保护机制 - 入侵检测和病毒检测:
将每个文件的Hash值 H(F) 存储在安全系统中,随后就能够通过重新计算 H(F) 来判断文件是否被修改过 - 构建随机函数(PRF)或用做伪随机发生器
Hash 函数安全性
- 原像:对于 Hash 函数 ,称 为 原像。
- 碰撞:因为 是多对一映射,所以对于任意给定的 Hash 值 ,对应有多个原像。如果满足 且 ,则称出现碰撞。
- 假设函数 的输入消息或数据块长度是 位,输出的长度为 位,且 ,则平均每个 Hash 值对应 个原像。
- 若输入长度不限,则每个hash值对应原像个数将更大。
Hash 函数的安全性需求
| 需求 | 描述 |
|---|---|
| 输入长度可变 | 可应用于任意大小的数据块 |
| 输出长度固定 | 产生定长的输出 |
| 效率 | 对于任意给定的 ,计算 比较容易,用软件和硬件均可实现 |
| 单向性 | 对于任意给定的 Hash 码 ,找到满足 的 在计算上是不可行的 |
| 抗弱碰撞性 | 对任意给定的分块 ,找到满足 且 的 在计算上是不可行的 |
| 抗强碰撞性 | 找到任何满足 的偶对 在计算上是不可行的 |
| 伪随机性 | 的输出满足伪随机性测试标准 |
※:一个函数如果是抗强碰撞的,那么同时也是抗弱碰撞的,单反之不一定成立。一个函数可以是抗强碰撞的,但不一定是抗原像攻击的,反之亦然;一个函数可以是抗弱碰撞的,但不一定是抗原像攻击的,反之亦然。
不同应用下的 Hash 函数的安全需求
| 抗原象攻击 | 抗弱碰撞攻击 | 抗强碰撞攻击 | |
|---|---|---|---|
| Hash+数字签名 | 是 | 是 | 是* |
| 入侵病毒和病毒检测 | 是 | ||
| Hash+对称加密 | |||
| 单向口令文件 | 是 | ||
| MAC | 是 | 是 | 是* |
※:标 * 处要求攻击者能够实现选择消息攻击
攻击 Hash 函数
-
Hash函数的安全性取决于其抗击各种攻击的能力。
-
攻击杂凑函数的原理是:伪造消息,使其与原来消息的杂凑码相同
-
常见的攻击方法:穷举攻击、密码分析
-
穷举攻击:不依赖于任何算法细节,仅与Hash值长度有关;
-
原像攻击和第二原像攻击(弱碰撞攻击)
-
碰撞攻击:
-
生日攻击法:没有利用Hash函数的结构和任何代数弱性质,只依赖于Hash值的长度。
-
中点交会攻击法:是生日攻击的一种变形,不比较Hash值,而是比较链中的中间变量,适用于攻击具有分组链结构的Hash方案。
-
-
-
密码分析:依赖于具体算法的设计缺点,主要集中在:
- 对迭代型Hash函数的压缩函数 的内部结构的分析,
- 试图找到能由 的单步执行产生碰撞的有效方法。
-
穷举攻击
第一类生日攻击
-
相关问题
已知一散列函数 H 有 n 个可能的输出,H(x) 是一个特定的输出,如果对 H 随机取 k 个输入,则至少有一个输入 y 使得 H(y)=H(x) 的概率为 0.5 时,k 有多大?
为叙述方便,称对散列函数 H 寻找上述 y 的攻击为第Ⅰ类生日攻击。 -
解答:
因为 有 个可能的输出,所以输入 产生的输出 等于特定输出 的概率是 ,即
的概率是
取 个随机值而函数的 个输出中没有一个等于 ,其概率等于每个输出都不等于 的概率之积,为 ,
所以, 取 个随机值得到函数的k个输出中至少有一个等于 的概率为 。
由 ,其中 ,可得
若使上述概率等于 ,则 。
特别地,如果 的输出为 比特长,即可能的输出个数 ,则 。
生日攻击
-
生日悖论
生日悖论是考虑这样一个问题:——在k个人中至少有两个人的生日相同的概率大于 时, 至少多大?
为了回答这一问题,首先定义下述概率:
设有 个整数项,每一项都在 到 之间等可能地取值,则 个整数项中至少有两个取值相同的概率为 。
生日悖论就是求使得 的最小 。 -
当 时,,即上述问题只需 23人,人数如此之少。
当 时,,即获得如此大的概率! -
之所以称这一问题是悖论,是因为当人数 给定时,得到的至少有两个人的生日相同的概率比想象的要大得多。这是因为在k个人中考虑的是任意两个人的生日是否相同,在23个人中可能的情况数为 。
-
生日攻击
-
生日攻击是基于下述结论:
设散列函数 有 个可能的输出(即输出长 比特),如果 的 个随机输入中至少有两个产生相同输出的概率大于0.5,则
称寻找函数H的具有相同输出的两个任意输入的攻击方式为第Ⅱ类生日攻击。
-
生日攻击法
生日悖论原理可用于构造对 Hash 函数的攻击:
设 Hash 函数值有 个比特, 是真消息, 是伪造的假消息,分别把消息 和 表示成 和 个变形的消息。消息与其变形消息具有不同的形式,但有相同的含义-
敌手可在文件的单词之间插入很多 space-space-backspace 字符对
-
使用意义相同但词句不同的语句
-
-
计算真消息 的变形与假消息 的变形发生碰撞的概率
由于 比特长的散列值共有 个,所以对于给定 的变形 和 的变形 , 与 不碰撞的概率是 。由于 共有 个变形,所以 的全部变形都不与 碰撞的概率是:
因为消息 共有 个变形,因此 的变形与 的变形都不碰撞的概率是:
的变形与 的变形发生碰撞的概率是:当 时,
-
步骤
② 敌手对 A 发送的消息M产生出 个变形的消息,每个变形的消息本质上的含义与原消息相同,同时敌手准备一个假冒消息 M’ ,并对假冒消息产生出 个变形的消息。
③ 敌手在产生的两个消息集合中,找出杂凑值相同的一对消息 和 ,由上述讨论可知敌手成功的概率大于 0.5。如果不成功,则重新产生一个假冒的消息,并产生 个变形,直到找到杂凑值相同的一对消息为止
④ 敌手将 提交给 A 请求签字,由于 与 的杂凑值相同,所以可将 A 对 的签字当作对 的签字,将此签字连同 一起发给意欲的接收者。
-
为了抵抗生日攻击,消息摘要必须足够长。建议Hash值长度至少为128 比特
-
中间相遇攻击
- 用于攻击一类具有特殊结构的Hash函数
- 分析Hash函数运算的中间值相等的概率
- 中间相遇攻击的基本原理为:
- 将消息分成两部分,对伪造消息的第一部分从初试值开始逐步向中间阶段产生r1个变量
- 对伪造消息的第二部分从Hash结果开始逐步退回中间阶段产生r2个变量。
- 在中间阶段有一个匹配的概率与生日攻击成功的概率一样。
迭代型散列函数
-
目前使用的大部分散列函数如 MD5,SHA,其结构都是迭代型的
-
迭代型 Hash 函数:Merkle 于1989 年提出:b 比特分组,n比特输出;f 为压缩函数,L 轮链接迭代
-
设 x 是一个长度为 L 个固定长度分组的比特串,重复应用压缩函数 f,对 x 进行多次压缩,最后得到 x 的散列值
-
关于分组:将输入消息 M 分为 L-1 个长度为 b 位的分组
-
填充:如果 L-1 组不足 b 位,则惊醒填充
-
附加:表示输入的总长度的分组
-
共 L 个长度为 b的分组
-
-
-
计算散列值的步骤
-
预处理:用一个公开算法在 x 右方填充,得到比特串 y,使 y 的长度为 n 的整数倍
即:
-
消息认证码
对消息认证的要求
-
攻击的类型
- 主动攻击
- 伪装、内容修改、顺序修改、计时修改
- 发送方否认、接收方否认
- 被动攻击
- 信息内容泄露
- 传输分析:分析双方的通信模式
- 主动攻击
-
认证是一个过程,验证所收到的消息确实来自真正的发送方,且是未被修改的消息,也可验证消息的顺序和及时性
消息认证函数
- 认证符的产生
- Hash:任意长的消息映射为定长的Hash值
- 消息加密:消息加密后的密文
- 消息认证码 MAC:消息和密钥的函数,产生定长的值
消息认证码 MAC
定义及使用方式
-
消息认证码 MAC 是一种消息认证技术,是指消息被一密钥控制的公开函数作用后产生的、用作认证符的、固定长度的数值,也称为密码校验和。
-
,其中, 为输入消息; 为 MAC 函数; 为共享的密钥; 为消息认证码。
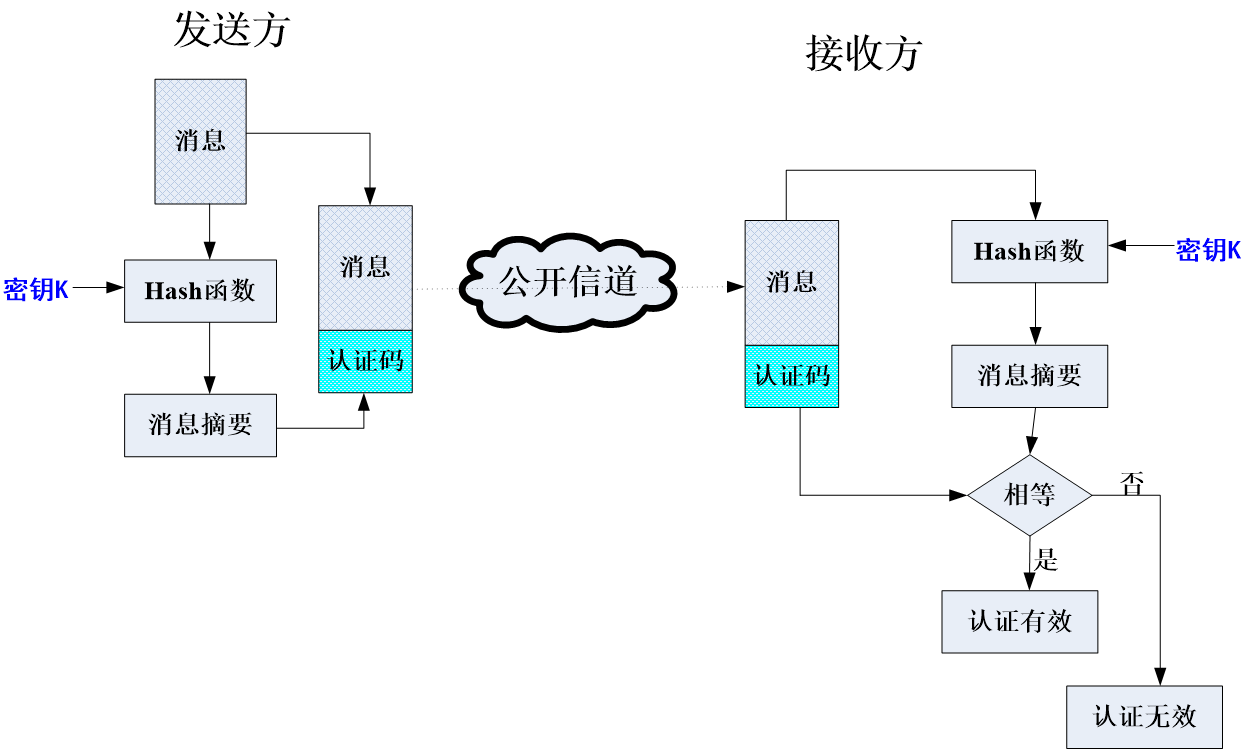
-
MAC 函数与加密类似,区别在于:MAC 算法不要求可逆性,而加密算法必须是可逆的。
-
为提供**保密性,**可在MAC函数以后(对整体)或以前(对 M)进行一次加密,而且加密密钥也需被收发双方共享
对消息认证码的要求
- 攻击目的
- 伪造攻击
- 密钥恢复攻击
密钥恢复攻击
-
产生MAC的函数一般都为多到一映射,如果产生 比特长的 MAC,则函数的取值范围为 个可能的 MAC,函数输入的可能的消息个数 ,而且如果函数所用的密钥为 比特,则可能的密钥个数为 。
-
如果系统不考虑保密性,即敌手能获取明文消息和相应的MAC,那么在这种情况下要考虑敌手使用穷搜索攻击来获取产生MAC的函数所使用的密钥。
-
攻击步骤
- 已知 ,其中 。对所有 个可能的密钥计算 ,得 个可能的密钥。
- 已知 ,其中 。对上一轮得到的 个可能的密钥计算 ,得 个可能的密钥。
如此下去,如果 ,则上述攻击方式平均需要 轮。
例如,密钥长为 80 比特,MAC长为 32 比特,则第 1 轮将产生大约 个可能密钥,第 2 轮将产生 个可能的密钥,第3轮即可找出正确的密钥。
伪造攻击
-
例如,设 是由 64 比特长的分组 链接得到的,其消息认证码由以下方式得到:
其中 表示异或运算,加密算法是电码本模式的 DES。
因此,密钥长为 56 比特,MAC长为 64 比特,如果敌手得到 ,那么敌手使用穷搜索攻击寻找 将需做 次加密。 -
敌手还可用以下方式攻击系统:
将 到 分别用自己选取的 到 替换,
求出 ,并用 替换
敌手可伪造一新消息 ,且 的MAC与原消息 的MAC相同。
阻止基于选择明文的穷举攻击
-
MAC应满足以下要求,其中假定敌手知道函数 ,但不知道密钥 :
如果敌手得到 和 ,则构造一满足 的新消息 在计算上不可行。 -
在以下意义下是均匀分布的:随机选取两个消息 ,
,其中 为 MAC 的长若 是 的某个变换,即 ,例如 为插入一个或多个比特,那么
认证算法对消息的某部分或位不应比其他部分或位更弱。
- 对MAC攻击时,因为攻击者需要有已选择的 <消息-MAC> 对或密钥信息,所以这种攻击方式不能离线进行。
MAC的构造
HMAC算法描述
H:嵌入的散列函数(如MD5、SHA),
M:HMAC的输入消息(包括散列函数所要求的填充位),
Yi(0≤i≤L-1):M的第i个分组,
L:M的分组数,
b:一个分组中的比特数,
n:由嵌入的散列函数所产生的杂凑值的长度,
K:密钥,如果密钥长度大于b,则将密钥输入到散列函数中产生一个n比特长的密钥,
K+是左边经填充0后的K,K+的长度为b比特,
ipad为b/8个00110110,
opad为b/8个01011010。
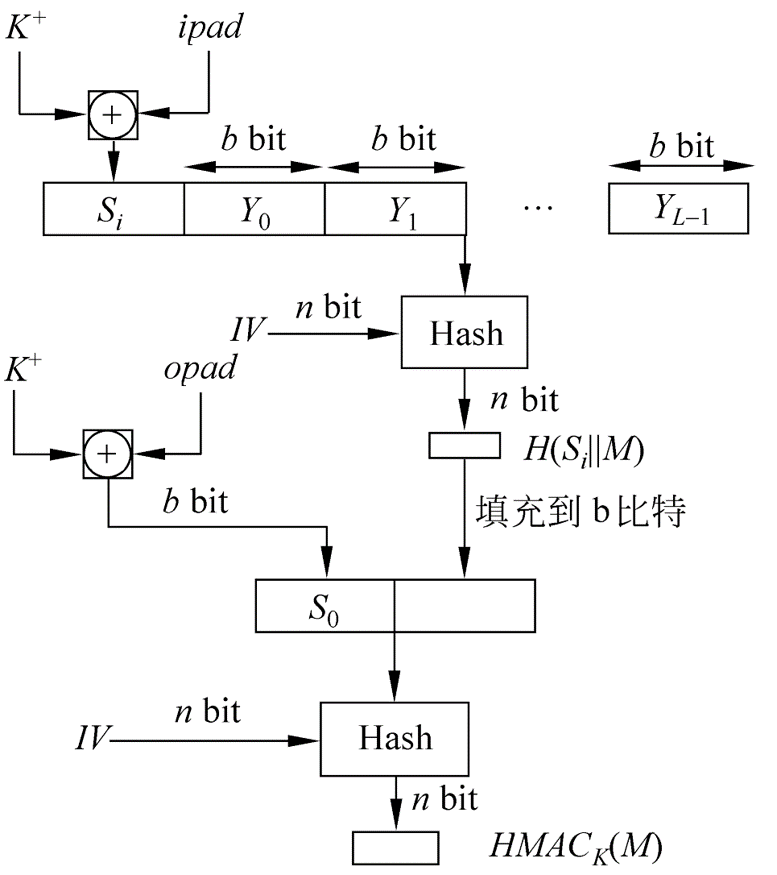
密钥管理和分发
对称加密的对称密钥分发
-
密钥可根据其不同用途分为会话密钥和主密钥两种类型
-
会话密钥又称为数据加密密钥
-
主密钥又称为密钥加密密钥
-
-
密钥由 A 选取并通过物理手段发送给 B
-
密钥由第三方选取并通过物理手段发送给A和B
※:第 1 和第 2 种方法称为人工发送,分配的代价很大
-
如果A、B事先已有一密钥,则其中一方选取新密钥后,用已有的密钥加密新密钥并发送给另一方
-
缺点:攻击者一旦获得一个密钥就可获取以后所有的密钥;
用这种方法对所有用户分配初始密钥时,代价仍然很大
-
-
如果 A 和 B 与第三方 C 分别有一保密信道,则 C 为 A、B 选取密钥后,分别在两个保密信道上发送给 A、B
- 该方法最常用
- 其中的第三方通常是一个负责为用户分配密钥的密钥分配中心(KDC)
- 这时每一用户必须和密钥分配中心有一个共享密钥,称为主密钥(可通过第二种方法)
- 通过主密钥分配给一对用户的密钥 称为会话密钥,用于这一对用户之间的保密通信
- 通信完成后,会话密钥即被销毁。如上所述,如果用户数为 ,则会话密钥数为 。但主密钥数却只需 个,所以主密钥可通过物理手段发送
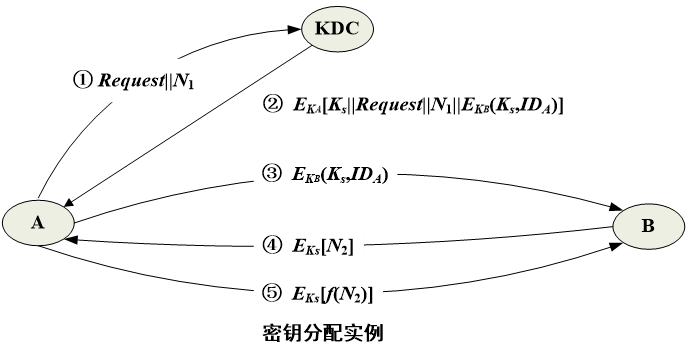
-
网络中如果用户数目非常多且分布的地域非常广,则需要使用多个KDC的分层结构
- 分层结构可减少主密钥的分布
- 分层结构还可将虚假KDC的危害限制到一个局部区域,但会降低信任度
-
会话密钥的有效期
- 更换得越频繁,系统的安全性就越高
- 更换得太频繁,又将延迟用户之间的交换,造成网络负担
-
用密钥分配中心为用户分配密钥时,要求所有用户都信任KDC,同时还要求对 KDC 加以保护。如果密钥的分配是无中心的,则不必有以上两个要求
非对称加密的对称密钥分发
- 公钥分配完成后,用户可用公钥加密体制进行保密通信。然而由于公钥加密的速度过慢,以此进行保密通信不太合适,但用于分配单钥密码体制的密钥却非常合适
- 简单分配:用公钥直接加密会话密钥
- 缺点:中间人攻击
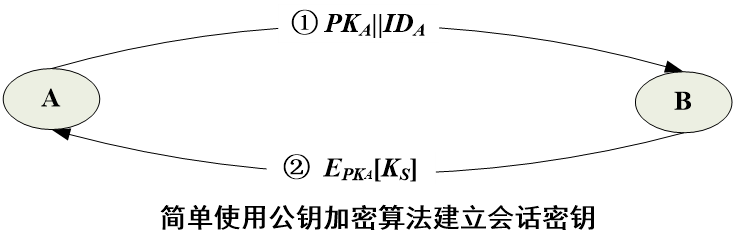
- 具有保密性和认证性的密钥分配
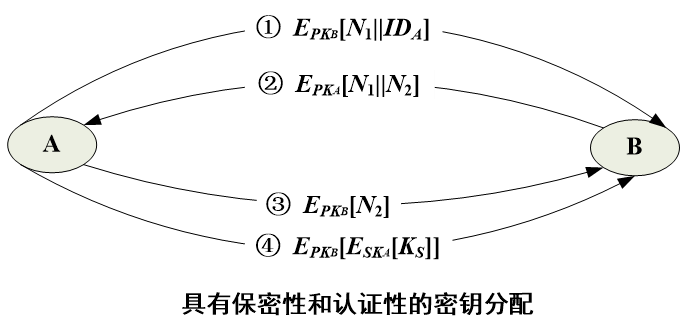
公钥分发
-
公开发布
- 用户将自己的公钥发给每一其他用户,或向某一团体广播
- 缺点:任何人都可伪造这种公开发布
-
公用目录表
- 公用目录表的建立、维护以及公钥的分布由某个可信的实体或组织承担,称这个实体或组织为公用目录的管理员
-
公钥授权
- 通过更加严格地控制目录中的公钥分配,使公钥分配更安全
- 优点:每次密钥的获得由公钥管理机构查询并认证发送,用户不需要查表,提高了安全性
- 缺点:公钥管理机构必须一直在线
-
公钥证书
-
用户通过公钥证书来互相交换自己的公钥而无须与公钥管理机构联系
-
X.509证书
-
公钥基础设施
- PKI 系统是有硬件、软件、人、策略和程序构成的一整套体系
- IETF 的 PKIX 工作组在 X.509 的基础上,建立一个可以构建网络认证的基本模型
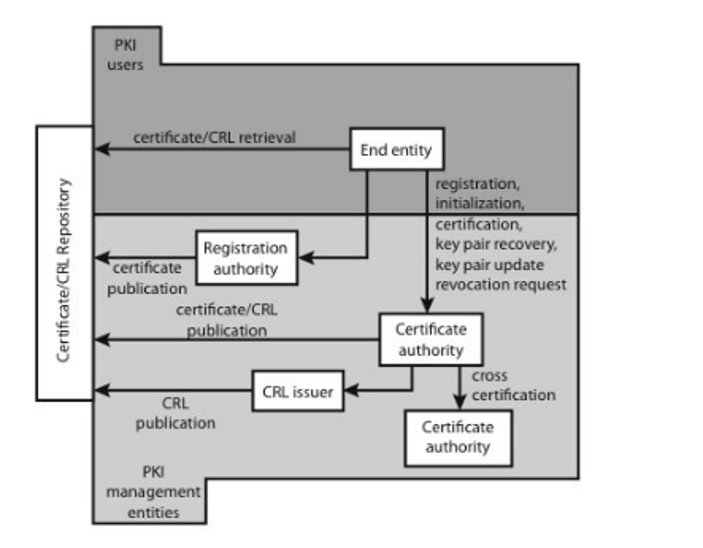
- PKI
- 端实体
- 签证机构 CA
- 注册机构 RA
- 证书撤销列表发布 CRL
- 证书存储库
- PKI 主要完成功能
- 为用户生成一对密钥,并通过一定途径分发给用户
- CA 为用户签发数字证书,形成用户的公开密钥信息,并通过一定的途径分发给用户
- 对用户证书进行有效性认证
- 对用户的数字证书进行管理,包括:有效证书的公布、册小证书的公布、证书归档等
- PKIX 管理任务
- 用户注册
- 初始化
- 认证
- 密钥对的恢复
- 密钥对的更新
- 证书撤销请求
- 交叉认证